Greens theorem-is this along the right line

[gtfitzpatrick]

Homework Statement

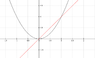
Cis the boundary of the region given by curves y = x^{2} and y=x use Greens theorem to evaluate the following line integrals.
a) \oint(6xy-y^2 )dx
b) \oint(6xy-y^2 )dy

Homework Equations

The Attempt at a Solution

so greens theorem states \oint Mdx + Ndy = \int\int \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y} dxdy

so for (a) M=6xy-y^2 N=0
The 2 curves intersect at (1,1)

so \oint (6xy-y^2)dx = \int^{1}_{0} \int^{x^2}_{x} (6x-2y) dydx
=\int^{1}_{0} -x^4 + 6x^3 -7x^2 dx
=\frac{-31}{30}

and for (b) N=6xy-y^2 M=0
The 2 curves intersect at (1,1)

so \oint (6xy-y^2)dy = \int^{1}_{0} \int^{x^2}_{x} (6y-2y)dydx
=\int^{1}_{0} 2x^4 - 2x^2 dx
=\frac{-4}{15}

am i doing this right?

 

[DryRun]

Always sketch the graph, to know the boundary of the region enclosed by the two curves. Check the attachment.

First, describe the region enclosed by the two curves (let's call it, region R).

For x fixed, y varies from $y = x^2$ to $y= x$
x varies from x = 0 to x = 1

Let's consider part (a). You have correctly recognized terms M and N. Now, you need to find:
$$\iint_R \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y} dxdy=\iint_R 0 - \frac{\partial M}{\partial y} dxdy=-\iint_R \frac{\partial M}{\partial y} dxdy$$
Set the limits:$$-\int_0^1 \int_{x^2}^x \frac{\partial M}{\partial y} dydx$$
You have to find: $$\frac{\partial M}{\partial y}=6x-2y$$
Thus, you get:$$-\int_0^1 \int_{x^2}^x (6x-2y) dydx=-\frac{11}{30}$$
Now, you should be able to do part (b).

 

[gtfitzpatrick]

Thanks sharks,
i think that cleared up a few things.
When i am doing part B do the limits change?as in...

\int_0^1 \int_{y}^{\sqrt{y}} (6y) dxdy

or do i keep the same limits?

 

[DryRun]

When i am doing part B do the limits change?as in...

\int_0^1 \int_{y}^{\sqrt{y}} (6y) dxdy

or do i keep the same limits?

Since the region of integration remains unchanged, you can use the same limits as in part (a).

Alternatively, you could also have defined the limits as:
$$\int_0^1 \int_{x^2}^x (6y) dydx$$but the answer should be the same.

 

[gtfitzpatrick]

Thanks sharks,I did it out both ways and got the same answer \frac{2}{5}

I have a similar question...

\oint (x^2 y)dx + (y+xy^2) dy between the curves y=x^2 and x=y^2

i sketched out the region and it very similar to the above question.

so from green theorem i get \int^{1}_{0} \int^{\sqrt{x}}_{x^2} y^2 - x^2 dydx which when i do it out i get 0. but from my sketch its not 0. am i taking the wrong limits?i've done it out 2 times. and got the same answer

 

[gtfitzpatrick]

\int^{1}_{0} \int^{\sqrt{x}}_{x^2} (y^2 - x^2) dydx

\int^{1}_{0} (\frac{1}{3} y^3 - x^2 y)^\sqrt{x}_{x^2} dx

\int^{1}_{0} (\frac{1}{3} x^{\frac{3}{2}} - x^{\frac{5}{2}} - \frac{1}{3}x^6 + x^4 dx

= (\frac{2}{15}x^{\frac{5}{2}} - \frac{2}{7}x^{\frac{7}{2}} - \frac{1}{21}x^{7} + \frac{1}{5}x^{5})^{1}_{0}

which works as zero...this can't be right?

 

[DryRun]

The answer is indeed 0. See the two attachments.