SUMMARY
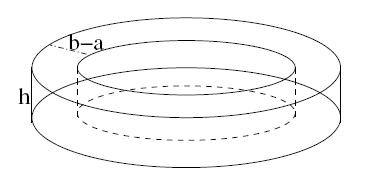
The discussion focuses on calculating the magnetic field strength (H) in a toroidal coil with a rectangular cross-section, consisting of N turns carrying a current I. The core material's magnetic permeability (\u) varies with the angle theta, defined as \u0=(1+k cos(theta))\u. The participants conclude that while the magnetic field B is dependent on the variable permeability and radius, the magnetic field strength H can be simplified to H=(I*N)/(2*π*r), indicating that H is independent of the core material's properties.
PREREQUISITES
- Understanding of electromagnetic theory, specifically magnetic fields and permeability.
- Familiarity with toroidal coil geometry and its parameters (inner radius, outer radius, height).
- Knowledge of the relationship between magnetic field strength (H), magnetic flux density (B), and permeability (\u).
- Basic proficiency in mathematical manipulation of equations involving trigonometric functions.
NEXT STEPS
- Study the derivation of magnetic field equations for toroidal coils.
- Explore the effects of varying magnetic permeability on magnetic field calculations.
- Learn about the applications of toroidal coils in inductors and transformers.
- Investigate advanced topics in electromagnetism, such as Maxwell's equations and their implications for magnetic fields.
USEFUL FOR
Students and professionals in physics and electrical engineering, particularly those focused on electromagnetism and magnetic field applications in toroidal systems.