SUMMARY
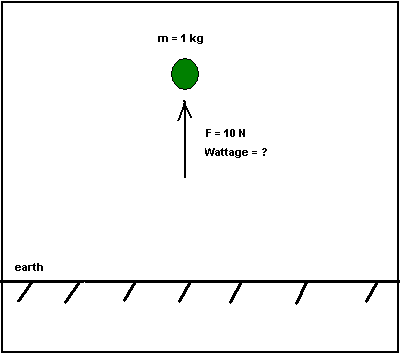
The discussion centers on the relationship between force, power, and motion, specifically regarding a 1 kg mass requiring a force of 10 Newtons to remain stationary. It is established that maintaining an object's position does not necessitate energy expenditure, as demonstrated by a bookshelf supporting an object without an energy source. The conversation highlights that while force is essential, the power required to generate that force depends on the method of propulsion, such as using a rocket motor or helicopter blades. The key takeaway is that there is no direct conversion from force to power without considering the object's velocity and the system's dynamics.
PREREQUISITES
- Understanding of Newton's Second Law (F = m × a)
- Basic principles of mechanics and energy
- Knowledge of power calculations (Watts and Joules)
- Familiarity with propulsion systems (e.g., rocket motors, helicopters)
NEXT STEPS
- Explore the relationship between force and power in mechanical systems
- Study the dynamics of helicopter lift and drag forces
- Investigate the principles of rocket propulsion and mass flow rates
- Learn about energy conservation in static and dynamic systems
USEFUL FOR
Physics students, engineers, and anyone interested in the principles of mechanics and propulsion systems will benefit from this discussion.