Having trouble figuring center of mass between Sun and Jupiter

[lancel916]

I am taking an astronomy class because I am interested in it and wanted to know more. I love all I am learning unfortunately my math skills are holding me back from getting all that I can out of this class. I realize this might not be the toughest math problem but can someone explain help me out with these two questions? The first question asks for R in terms of d1. I'm not sure what this means.

The Sun is 1,047 times more massive than Jupiter. Call the mass of the Sun m1 and that of Jupiter m2. The ratio m1/m2 is then 1,047. If the first equation is divided through by m2, we find that d2 = 1,047 d1, The Sun moves around the center of mass for the Sun-Jupiter system in an orbit about one thousand times smaller than Jupiter’s orbit. This motion for the Sun is small but not insignificant.

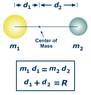
m1 d1 = m2 d2
d1 + d2 = R

Using the second equation, what is R in terms of d1 given the value of d2 above? R=_____d1

If R, the total distance between the Sun and Jupiter, is 7.783 x 108 km (5.2 AU), what is d1 in km? d1= _____km

 

[Drakkith]

Please show any work you've already done and explain where exactly you start to have trouble. Also, future homework questions should be posted in the Homework subforum.
As for showing R in terms of D1, it looks like they want you to find D1 and show it as something like R= 1.5D1 or something.

 

[lancel916]

Well I figured m1 = 1,047 and m2 = 0 since the Sun is 1,047x larger than Jupiter. Then I took d1 as 1 and d2= 1/1,047 which is .000955. But R= 1.000955 d1 doesn't seem right at all. I think I am plugging the wrong numbers into the equation.

 

[HallsofIvy]

The center of mass between mass M1 and mass M2, with distance d between them, is the point on a support between them where they would balance on a fulcrum (a strange concept for the sun and Jupiter, I will admit!). If we set the fulcrum at distance x1 from M1 and let x2 be the distance from the fulcrum to M2, the fact that they balance means that the torques must be the same: M1x1= M2x2. We also have, of course, x1+ x2= d so we have two equations to solve for x1 and x2. From x1+ x2= d, x2= d- x1. Putting that into the first equation, M1x1= M2(d- x1)= dM2- M2x1.
Then M1x1+ M2x2= (M1+ M2)x1= dM2 so that x1= (dM2)/(M1+ M2). x2= d- x1= d- dM1/(M1+ M2)= [d(M1+ M2)- dM1)/(M1+ M2)= dM1/(M1+M2).

If the sun is 1047 times the mass of Jupiter, then you had better take the mass of Jupiter equal to 1, not 0. 1047 times 0 is also 0!

You say "The first question asks for R in terms of d1. I'm not sure what this means." No one can know what it means if you don't tell us what d1 and R mean! Do you mean that R is the distance from the sun to Jupiter and d1 is the distance from the sun to the center of mass? Assuming that we have d1= R(1)/(1047+1)= (1/1048)R and then d2= R- R/1048= (1047/1048)R

 

[lancel916]

OK so that makes sense. So then part a would be R= 1048 d1

So then if R (the total distance between the Sun and Jupiter) is 7.783 x 10⁸ km, what is d1 in km?
Would you take 778300000 and divide by 1048?

 

[lancel916]

Thank you so much for your help! I just checked my first answers and they are correct.

R= 1048 d1

d1= 742652.67 km

 

[!)("/#]

The center of mass expression is defined by the following:

\overline{R} = \frac{\sum_i^n \overline{x}_i m_i}{ \sum_i^n m_i }

Where x_i are the positions of the particles, an m_i are the mases of these particles.

In your example you have to do the following:

|\overline{R}_{sj}| = \frac{x_j m_j + x_s m_s}{m_j + m_s}

Where x_j is the position of jupiter, also m_j the mass of it, and in the other hand you have the position of the sun x_s and the mass of it m_s.