- #1
riddle_me_phys
- 10
- 0
Hey all,
I'm brushing up on some physics in my spare time, and I was wondering if someone knowledgeable here could help me clarify the reasons behind a couple answers...much thanks in advance! =)
Question 1) The greatest linear acceleration of the center of mass of a baseball bat will be produced by pushing with a force F at...(picture attached)
Relevant equation: Force = mass[itex]_{center of mass}[/itex] * acceleration[itex]_{center of mass}[/itex]
Attempt at solution: The solution tells me that it's "D) all the same," and that using F = ma, you can see that linear acceleration is not related to the position where the force is applied. However, this doesn't seem intuitive to me.
If I have a bat sitting on a table, and I push at position 1 or 3, I would have expected there to be some but less linear acceleration (and more rotational acceleration), so that position 2 would have the greatest linear acceleration. I remember reading that rotational acceleration is calculated independently of linear acceleration.
Am I overanalyzing and treating this as more than a statics problem? That as soon as it starts rotating if pushed in position 1 or 3, that the scenario is no longer valid because, realistically force F (if it continues in the same direction) is no longer pushing at the bat perpendicular to its motion? So in that case, I should think of this force more like a quick, impulsive force than a force over a prolonged period of time?
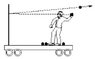
Question 2) Suppose you are on a cart, initially at rest on a track with very little friction. You throw balls at a partition that is rigidly mounted on the cart. If the balls bounce straight back as shown in the figure, is the cart put in motion? (image attached)
Relevant equation:
Conservation of momentum: 0 = m_person+cart* v_person+cart + m_ball * v_ball
Attempt at solution: Taking the person, cart and balls as a system, there are no external forces in the direction of motion and we can say that momentum is conserved. The solution tells me that the answer is "A) it moves to the left." Again, if I use the equation to answer, I arrive at that conclusion. Or if I imagine putting a curtain covering the contraption and the only thing I see is a ball bouncing out, I can visualize that that must make the cart move to the left. HOWEVER...
If I analyze it from the following approach, I get stuck (probably overanalyzing it again). Let's say the person starts out with the ball in his hand, primed to throw it (he's like a gun). He throws it, and the ball goes to the left, so the cart + person goes to the right in response (like recoil). Then the ball hits the cart partition and bounces off elastically. How do you justify that after that action the cart + person move to the left (and doesn't just stop the cart)? If anything, doesn't the ball hit the wall with a force F (that it left the person's hand in), and cancel it out?
In a variation of this problem, I was told that if the ball is inelastic and smashes/sticks to the wall instead of bouncing off, that in this case the cart would stop moving to the right once the ball hits the wall.
??
Again, any clarification would be great and super appreciated! =)
I'm brushing up on some physics in my spare time, and I was wondering if someone knowledgeable here could help me clarify the reasons behind a couple answers...much thanks in advance! =)
Question 1) The greatest linear acceleration of the center of mass of a baseball bat will be produced by pushing with a force F at...(picture attached)
A) position 1
B) position 2
C) position 3
D) all the same
E) not enough information
Relevant equation: Force = mass[itex]_{center of mass}[/itex] * acceleration[itex]_{center of mass}[/itex]
Attempt at solution: The solution tells me that it's "D) all the same," and that using F = ma, you can see that linear acceleration is not related to the position where the force is applied. However, this doesn't seem intuitive to me.
If I have a bat sitting on a table, and I push at position 1 or 3, I would have expected there to be some but less linear acceleration (and more rotational acceleration), so that position 2 would have the greatest linear acceleration. I remember reading that rotational acceleration is calculated independently of linear acceleration.
Am I overanalyzing and treating this as more than a statics problem? That as soon as it starts rotating if pushed in position 1 or 3, that the scenario is no longer valid because, realistically force F (if it continues in the same direction) is no longer pushing at the bat perpendicular to its motion? So in that case, I should think of this force more like a quick, impulsive force than a force over a prolonged period of time?
Question 2) Suppose you are on a cart, initially at rest on a track with very little friction. You throw balls at a partition that is rigidly mounted on the cart. If the balls bounce straight back as shown in the figure, is the cart put in motion? (image attached)
A) it moves to the right
B) it moves to the left
C) it remains in place
D) not enough information
Relevant equation:
Conservation of momentum: 0 = m_person+cart* v_person+cart + m_ball * v_ball
Attempt at solution: Taking the person, cart and balls as a system, there are no external forces in the direction of motion and we can say that momentum is conserved. The solution tells me that the answer is "A) it moves to the left." Again, if I use the equation to answer, I arrive at that conclusion. Or if I imagine putting a curtain covering the contraption and the only thing I see is a ball bouncing out, I can visualize that that must make the cart move to the left. HOWEVER...
If I analyze it from the following approach, I get stuck (probably overanalyzing it again). Let's say the person starts out with the ball in his hand, primed to throw it (he's like a gun). He throws it, and the ball goes to the left, so the cart + person goes to the right in response (like recoil). Then the ball hits the cart partition and bounces off elastically. How do you justify that after that action the cart + person move to the left (and doesn't just stop the cart)? If anything, doesn't the ball hit the wall with a force F (that it left the person's hand in), and cancel it out?
In a variation of this problem, I was told that if the ball is inelastic and smashes/sticks to the wall instead of bouncing off, that in this case the cart would stop moving to the right once the ball hits the wall.
??
Again, any clarification would be great and super appreciated! =)