Raz91
- 20
- 0
Hello ,
I tried to solve this coupled ODE but with no success
Does anyone know if there is an analytical solution to this equation?
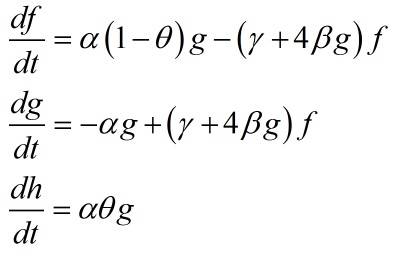
my problem is with the first & the second equations the term g*f is the my biggest problem i think
once i have the solution for g - the solution for h is trivial.
THANK YOU!
I tried to solve this coupled ODE but with no success
Does anyone know if there is an analytical solution to this equation?
my problem is with the first & the second equations the term g*f is the my biggest problem i think
once i have the solution for g - the solution for h is trivial.
THANK YOU!
