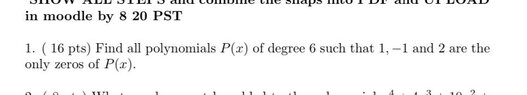MHB Help Desk - Get Answers to Your Questions

  • Thread starter Thread starter Tstuvshu
  • Start date Start date
Click For Summary
The discussion centers on constructing a sixth-degree polynomial with specific factors and characteristics. It emphasizes that multiple polynomials can meet the criteria, including repeated linear factors and a quadratic factor without real roots. The essential factors identified are (x - 1), (x + 1), and (x - 2), but additional factors must be included to reach the required degree. Various combinations of these factors, such as $(x- 1)^4(x- 2)(x+ 1)$ or $(x-1)^2(x- 2)^2(x+ 1)^2$, are suggested. Additionally, any non-zero constant can be multiplied with the product of these factors.
Tstuvshu
Messages
1
Reaction score
0
Need help please
 

Attachments

  • 9FF5AA8D-6343-430C-9780-528FCA5691C6.jpeg
    9FF5AA8D-6343-430C-9780-528FCA5691C6.jpeg
    14.2 KB · Views: 104
Physics news on Phys.org
Any product of (x - 1), (x + 1), (x - 2) and a constant, with some repeated linear factors, quadratic factor without any real roots, or irreducible cubic factor that has 1, -1 or 2 as its roots.
 
What kind of "help" do want? For one thing, there is no single answer. There are many polynomials that satisfy these conditions! The only factors must be (x- 1), (x+ 1), and (x- 2) but that is only three and for a sixth degree polynomial you need six so some factors must be repeated. That could be $(x- 1)^4(x- 2)(x+ 1)$ or $(x-1)^2(x- 2)^2(x+ 1)^2$ or any combination of exponents that add to six. Also, the product of factors can be multiplied by any non-zero constant.
 

Thread 'Proving that convexity implies second order derivative being positive'

There are probably loads of proofs of this online, but I do not want to cheat. Here is my attempt: Convexity says that $$f(\lambda a + (1-\lambda)b) \leq \lambda f(a) + (1-\lambda) f(b)$$ $$f(b + \lambda(a-b)) \leq f(b) + \lambda (f(a) - f(b))$$ We know from the intermediate value theorem that there exists a ##c \in (b,a)## such that $$\frac{f(a) - f(b)}{a-b} = f'(c).$$ Hence $$f(b + \lambda(a-b)) \leq f(b) + \lambda (a - b) f'(c))$$ $$\frac{f(b + \lambda(a-b)) - f(b)}{\lambda(a-b)}...
View full post »

Similar threads

MHB Calc Solved! Get Quick Help With Your Calculus Q
  • · Replies 1 ·
Replies
1
Views
1K
MathHelpBoards.com merges with PF
  • · Replies 42 ·
2
Replies
42
Views
5K
MHB Using advanced calculus for finding values
  • · Replies 2 ·
Replies
2
Views
1K
MHB Solve Calculus Problem: Answers to d, e, f in Math Paper
  • · Replies 3 ·
Replies
3
Views
1K
MHB Finding Limit: Get Step-by-Step Help Here
  • · Replies 1 ·
Replies
1
Views
1K
MHB Another Limit, without L'hospital rule
  • · Replies 6 ·
Replies
6
Views
2K
Graduate Solve Line Integral Question | Get Math Help from Physics Forums
  • · Replies 5 ·
Replies
5
Views
2K
MHB Confused: Seeking Help on Problem Solution
  • · Replies 2 ·
Replies
2
Views
1K
MHB What Is the Total Distance Traveled by the Particle from t = 0 to t = 3?
  • · Replies 4 ·
Replies
4
Views
2K
MHB Find the global extrema of this function over the given region
  • · Replies 10 ·
Replies
10
Views
3K