Help finding a triangle inside a triangle

[aheight]

TL;DR

Finding precise location of triangle in a right triangle with the give conditions

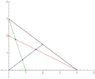
I would like to find the triangle $\bigtriangleup DEF$ in the plot below that is inside the right triangle $\bigtriangleup ABC$ given $\overline{AB}=3, \overline{AC}=4$ with $\overline{BD}=\overline{DE},\overline{AE}=\overline{EF}, \overline{FC}=2\overline{DF}$. However, I'm finding it difficult to actually find precisely in the larger triangle where it is (diagram below is only approx.) . Surely if I let $D=(x_3,y_3),F=(x_2,y_2), E=(x_1,y_1)$ as per the diagram and solve the following six simultaneous equation for the coordinates of D,E, and F inside the larger triangle should do it but when I attempt to numerically solve the equations (in Mathematica), I obtain the empty set. However, the triangle does exist. I was wondering if someone could look at my work and confirm that I have a valid set of equations to find these points? For example, the first equation is obtained by noting:
$x_1^2+y_1^2=z^2$ and $(x_2-x_1)^2+(y_2-y_1)^2=z^2$ and so forth.

Thanks guys.

$$\begin{array}{l}
x_1^2+y_1^2=(x_2-x_1)^2+(y_2-y_1)^2 \\
x_3^2+(3-y_3)^2=(x_3-x_1)^2+(y_3-y_1)^2 \\
4[(x_3-x_2)^2+(y_3-y_2)^2]=(4-x_2)^2+y_2^2 \\
x_2^2+y_2^2=4(x_1^2+y_1^2)\\
4[x_3^2+(3-y_3)^2]=x_1^2+(3-y_1)^2\\
9[(x_3-y_2)^2+(y_3-y_2)^2]=(4-x_3)^2+y_3^2
\end{array}
$$

 

[Delta2]

I didn't check your equations thorously but I think the reason that mathematica can't solve it, is that the system probably has infinite solutions. I think if you manually enter coordinates for say (x1,y1) and leave x2,y2 and x3,y3 as unknowns, mathematica will be able to solve it.

 

[pbuk]

the triangle does exist

How do you know this?

$(x_3−y_2)^2$

Doesn't look right.
[Edit: $\LaTeX$ corrected]

 

[Delta2]

How do you know this?

I think from the scheme is obvious that for this right triangle ABC it exists at least one DEF triangle.

Moreover I think that for any right triangle there exist infinite triangles DEF which "oscillate" around a "central" DEF_0 triangle.

To see this pick any line from B that intersects the side AC at an internal point. Then we can choose randomly a point D on this line and then choose a point E such that BD=DE. Now within a range of angles that the line BD makes with side AB and within a range of magnitude of BD, we can choose point F such AE=EF and E,F are internal to the triangle ABC (they will not be internal for all angles and for all lengths of BD, but within a range of those ,E,F will be internal) so the triangle DEF will be internal.

EDIT: BIG OOPS, i overlooked that we also have the restriction FC=2DF, this might make the triangle non existant...

 

[aheight]

Here's the solution guys (I had an error in the Solve parameters initially). I believe there is only one solution. And here's the Mathematica code I used to solve it (Solve took 30 minutes to find the solution). Also, I confirmed the answer by computing the area via Heron's formula against the known area of 3/5.

[CODE title="Mathematica code"](* takes about 40 minutes to find the solutions below *)
r1 = Polygon[{{0, 0}, {0, 3}, {4, 0}}];
eqn1 = x1^2 + y1^2 == (x2 - x1)^2 + (y2 - y1)^2;
eqn2 = x3^2 + (3 - y3)^2 == (x3 - x1)^2 + (y3 - y1)^2;
eqn3 = 4 ((x3 - x2)^2 + (y3 - y2)^2) == (x2 - 4)^2 + y2^2;
eqn4 = x2^2 + y2^2 == 4 (x1^2 + y1^2);
eqn5 = 4 (x3^2 + (3 - y3)^2) == x1^2 + (3 - y1)^2;
eqn6 = 9 ((x3 - x2)^2 + (y3 - y2)^2) == (4 - x3)^2 + y3^2;
Solve[{eqn1 && eqn2 && eqn3 && eqn4 && eqn5 && eqn6 &&
Element[Alternatives @@ {{x1, y1}, {x2, y2}, {x3, y3}}, r1]}, {x1,
x2, x3, y1, y2, y3}][/CODE]

{{x1->4/5,x2->8/5,x3->2/5,y1->3/5,y2->6/5,y3->9/5}}

 

[Bill Simpson]

This takes a fraction of a second to find a solution

Clear["Global`````*"]; (*I cannot make it display just and only one grave followed by asterisk*)
a={0,0}; b={0,3}; c={4,0}; d={dx,dy}; e={ex,ey}; f={fx,fy};
Reduce[b-d==d-e && a-e==e-f && f-c==2(d-f), {dx,dy,ex,ey,fx,fy}]
  (*which returns*)
dx==2/5 && dy==9/5 && ex==4/5 && ey==3/5 && fx==8/5 && fy==6/5

  (*check the result*)
{b-d==d-e, a-e==e-f, f-c==2(d-f)}/.{dx->2/5, dy->9/5, ex->4/5, ey->3/5, fx->8/5, fy->6/5}
(*which returns*)
  {True,True,True}