- #1
General_Sax
- 446
- 0
Help me understand a homework solution -- intro to ring theory -- ideals
problem:
solution:
The first paragraph is just saying the ideals generated by the units in the ring is the whole ring correct?
Also, the principal ideals generated by 2, 4 and 8 are all the same correct? So those are three ideals or just one?
So, in the final answer there are 4 ideals in total right?
And finally why do we care about Ideals so much? What use do they even have besides giving students of average intelligence a giant headache in intro abstract algebra course lol?
problem:
Determine all ideals of Z/Z10.
solution:

the solution is continued on
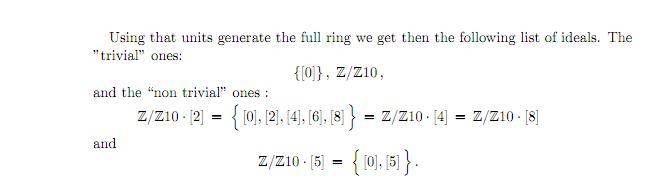
The first paragraph is just saying the ideals generated by the units in the ring is the whole ring correct?
Also, the principal ideals generated by 2, 4 and 8 are all the same correct? So those are three ideals or just one?
So, in the final answer there are 4 ideals in total right?
And finally why do we care about Ideals so much? What use do they even have besides giving students of average intelligence a giant headache in intro abstract algebra course lol?