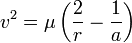SUMMARY
The discussion focuses on deriving the delta-v equations for Hohmann transfer orbits, specifically the mathematical steps involved in calculating the change in velocity required for such transfers. The user presents equations for v1 and v2, which relate to the velocities at two different orbits, and attempts to manipulate these to find delta-v. Key equations include v1² = u (2/r1 - 1/a) and v2² = u (2/r2 - 1/a), leading to the expression for delta-v as (delta v)² = mu(2/r2 - 1/a) - mu sqrt((2/r2 - 1/a)(2/r1 - 1/a)). The user seeks assistance in simplifying the resulting expression involving the semi-major axis 'a' and other variables.
PREREQUISITES
- Understanding of orbital mechanics and Hohmann transfer orbits
- Familiarity with gravitational parameters, specifically the standard gravitational parameter (mu)
- Proficiency in algebraic manipulation and simplification of equations
- Basic knowledge of LaTeX for mathematical typesetting
NEXT STEPS
- Study the derivation of Hohmann transfer orbits in detail, focusing on the equations for v1 and v2
- Learn about the standard gravitational parameter (mu) and its applications in orbital mechanics
- Practice algebraic techniques for simplifying complex equations, including partial fractions
- Explore LaTeX typesetting for mathematical expressions to improve clarity in communication
USEFUL FOR
Aerospace engineering students, physics enthusiasts, and anyone involved in orbital mechanics or space mission planning will benefit from this discussion.