How can a horizontal component be of sin? Error in book or my brain?

[Tangeton]

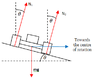
I've learned that the horizontal component is F cos angle not F sin angle, but I'm looking right now into the aqa physics a student book from nelson thrones, chapter 2.3 page 27, and it says that the horizontal components going to be made up of sin and the vertical out of cos... This is about banking of the road and I have a diagram of a F1 racing car on a banked surface, and it says that the normal forces on the tires from the banked surface (N1 and N2) have horizontal components of (N1 + N2) Sin angle and vertical components (N1 + N2) Cos angle but how is that possible :(

Is the mistake in the book or are sin and cos not always vertical and horizontal components respectively?

 

[Domenico94]

Maybe it's only in that particular case..

 

[256bits]

Hmmm.
Which angle do you, or the book, specify?

The road is banked at an angle 'alpha' from the horizontal.
The normal would be then, by high school geometry, at an angle of 'alpha' from the vertical.

Or perhaps the other angle of a right triangle,
beta = 90 - alpha.

Draw a diagram.
Using alpha or beta will give an answer that either, follows a rule that you have found out is not cast is stone as one would wish, or what is written in the book.

 

[Tangeton]

Hmmm.
Which angle do you, or the book, specify?

The road is banked at an angle 'alpha' from the horizontal.
The normal would be then, by high school geometry, at an angle of 'alpha' from the vertical.

Or perhaps the other angle of a right triangle,
beta = 90 - alpha.

Draw a diagram.
Using alpha or beta will give an answer that either, follows a rule that you have found out is not cast is stone as one would wish, or what is written in the book.

I've placed a diagram in attachments.

 

[jtbell]

I've learned that the horizontal component is F cos angle not F sin angle

If the angle is measured from the horizontal (call it β), then the horizontal component is F cos β. If the angle is measured from the vertical (call it θ this time, as for N₁ and N₂ on your attached diagram), then the horizontal component is F sin θ. The two formulas give the same result because:

F sin θ = F sin (π/2 - β) = F cos β

 

[Dale]

I've learned that the horizontal component is F cos angle not F sin angle

As others have said, that depends if the angle is measured from the vertical or the horizontal. Also, sometimes you are not breaking a force into vertical and horizontal components, sometimes you are breaking it into components parallel or perpendicular to a surface, and sometimes the angle is measured parallel to the surface and sometimes the angle is measured perpendicular to the surface. There are too many possible combinations, so I made one simple rule that always works:

Imagine what happens as the angle goes to 0: if the component goes to 0 then sin(0)=0 so it is sin, if the component goes to the maximum then cos(0)=max so it is cos.

 

[CWatters]

Try completing the diagrams by adding dotted lines to represent the horizontal and vertical components. Then do the trig.

 

[sophiecentaur]

I've learned that the horizontal component is F cos angle not F sin angle,

Your problem is that you appear to have rote learned 'learned' a piece of information, rather than seeing why, in the case you were originally given, that you use Sin, rather than Cos.
As with all Physics problems involving Maths, the Maths you use will depend upon the physical situation and that's the bit you need to sort out first -i.e. the situation leads to the equation.

 

[Dmd7d4]

Like Sophie, I think you memorized the vertical and horizontal bit.

Like others have eluded to, arbitrary coordinate systems are not important. The relative position of the sides of the triangle vs the angle in question are what matter.

Just remember:
Sin(angle) = opposite / hypotenuse
Cos(angle) = adjacent / hypotenuse
Tan(angle) = opposite / adjacent

Pretty good tips here:
http://www.mathsisfun.com/sine-cosine-tangent.html

-Dave

 

[sophiecentaur]

I have often suggested the following to students with this same confusion:
You can often look at a setup and do a visual analysis to help you get started.
Assuming the geometry is straightforward, see (visual estimate) if the force will increase or decrease as you increase the angle. If it increases with angle then you are dealing with Sin and if it decreases then you are dealing with Cos.
Sometimes there may be a Tan involved but you can spot that if you can predict that a resulting force will get bigger and bigger and bigger- but you can usually look elsewhere in the diagram for another force that will avoid piling in with a Tan.