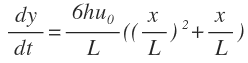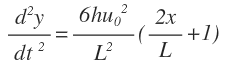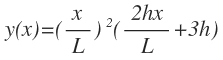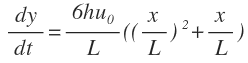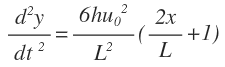Discussion Overview
The discussion revolves around the application of the chain rule in calculus, specifically in the context of differentiating a function related to the motion of an airliner. Participants are exploring how to correctly apply differentiation techniques, including the chain rule and product rule, to derive expressions for velocity and acceleration.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant expresses confusion about applying the chain rule to a specific function and seeks assistance in identifying errors in their approach.
- Another participant suggests assuming a relationship between variables, specifically that \( x = t \), to simplify differentiation.
- Concerns are raised about the complexity of expressions resulting from differentiation, with one participant mentioning difficulties in choosing appropriate variables for differentiation.
- Participants discuss the importance of recognizing common factors in expressions to simplify calculations before applying differentiation rules.
- One participant shares a derived expression for the first derivative, agreeing with an earlier posted result, and encourages others to try deriving it themselves.
- Another participant highlights the need for clarity in differentiating terms and suggests that separating sums before applying differentiation rules may simplify the process.
- There is a mention of the emotional impact of struggling with calculus, with one participant sharing personal challenges related to focusing on details during problem-solving.
- Participants discuss strategies for prioritizing operations in calculus, emphasizing the importance of recognizing when to combine like terms and the timing of applying differentiation rules.
Areas of Agreement / Disagreement
Participants generally agree on the need to apply the chain rule and other differentiation techniques correctly, but there is no consensus on the best approach to take or the specific errors made in the original problem. Multiple viewpoints on how to simplify and differentiate the expressions remain present.
Contextual Notes
Some participants note the complexity of the expressions and the potential for confusion when applying differentiation rules, indicating that the discussion may be limited by individual interpretations of the rules and the specific problem context.