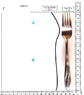
SUMMARY
The discussion focuses on determining the center of mass of a fork with varying thickness. Participants suggest breaking the fork into simpler geometric shapes, such as rectangles and triangles, to facilitate calculations. The symmetry of the fork along one axis is noted as a beneficial factor in the analysis. Approximations, such as treating the top part of the fork as rectangular and the connecting part as an angled board, are recommended to simplify the problem-solving process.
PREREQUISITES
- Understanding of basic geometry, including shapes like rectangles and triangles.
- Familiarity with the concept of center of mass and its calculation.
- Knowledge of symmetry in geometric objects.
- Ability to apply approximations in mathematical modeling.
NEXT STEPS
- Research methods for calculating the center of mass of composite shapes.
- Learn about the principles of symmetry in physics and engineering.
- Explore approximation techniques in mathematical modeling.
- Study the application of calculus in determining center of mass for irregular shapes.
USEFUL FOR
Students in physics or engineering courses, educators teaching mechanics, and anyone involved in the design or analysis of objects with varying geometries.