How can I rotate a coordinate system and write functions in the rotated system?

[Gackhammer]

Hey

So, I was wondering how to convert from one coordinate axes to another... in particular, where the new axes are y = x and y = -x, as seen by the picture below

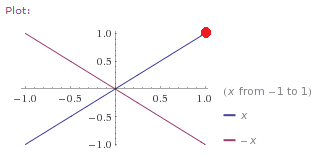
I want it so that the Red dot in the new coordinate system will be (\sqrt2,0). Is there an easy way to do this? (My lookings on the internet have not come up with anything good yet)

EDIT: Ok, I just found the equations to rotate, but I was wondering how I can write functions in this rotated coordinate system (Im trying to relate this to my recurrences work/fixed point stuff). I am trying to rotate the coordinate system then find the zeros in the rotated coordinate system to find the fixed points of the function

 

[Vorde]

Find formulas to transform your old parameters (x & y) into your new ones, and then substitute one for the other in equations.

Are you sure a rotation will be enough for you? (A.K.A., what x,y point do you want to be mapped to your new point root(2),0 ?)

 

[HallsofIvy]

Vorde's point is that the distance from (0, 0) to (1, 0) is, of course, 1 while the distance from (0, 0) to your red point is \sqrt{2}. You will need an expansion as well as a rotation.

x'= x- y, y'= x+ y will map (1, 0) to (1, 1) and map (0, 1) to (-1, 1).
That is, essentially, a rotation by 45 degree, counter-clockwise and a multiplication by \sqrt{2}.

You could have gotten those relations more easily by seeing that they must be linear, of the form x'= ax+ by and y'= cx+dy, since you do not want one part of the plane "stretched" or "squeezed" more than another. Further, you want (1, 0) to be mapped to (1, 1) so 1= a(1)+ b(0) and 1= c(1)+ d(0) giving a= 1, c= 1. You also want (0, 1) mapped to (-1, 1) so -1= a(0)+ b(1) and 1= c(0)+ d(1) giving b= -1, d= 1: x'= x- y, y'= x+ y as I said.