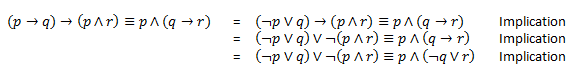werebilby
- 4
- 0
Hello Everyone,
This is my first post, so please me kind :D
I have an assignment and have been stuck on this thing for 2 days. I have no problems working this out with a truth table but we are not allowed to use this. So this it the expression.
View attachment 5619
I understand that I have to remove the implication but this doesn't really make sense to me and I have been using Youtube etc to try and get more info but just doesn't make sense as to how to apply the Laws of Logic. Help please?!
Regards
Werebilby
This is my first post, so please me kind :D
I have an assignment and have been stuck on this thing for 2 days. I have no problems working this out with a truth table but we are not allowed to use this. So this it the expression.
View attachment 5619
I understand that I have to remove the implication but this doesn't really make sense to me and I have been using Youtube etc to try and get more info but just doesn't make sense as to how to apply the Laws of Logic. Help please?!
Regards
Werebilby