How Can One Demonstrate the Ratio Between the Hypotenuses of Two Triangles?

[Kobzar]

Hello, everybody:

I am a philologist who is fond of mathematics, but who unfortunately has just an elementary high school knowledge of them. I am translating La leçon de Platon, by Dom Néroman (La Bégude de Mazenc, Arma Artis, 2002), which deals with music theory and mathematics in the works of Plato. The problem which brings me here is not about translation, but about mathematics. It is a long and complex one, so please take your time for examining it. Just in case, I am attaching a PDF document with my problem, to avoid any confusion with the reading of the mathematical expressions below.

On p. 93 of that book, there is this figure:

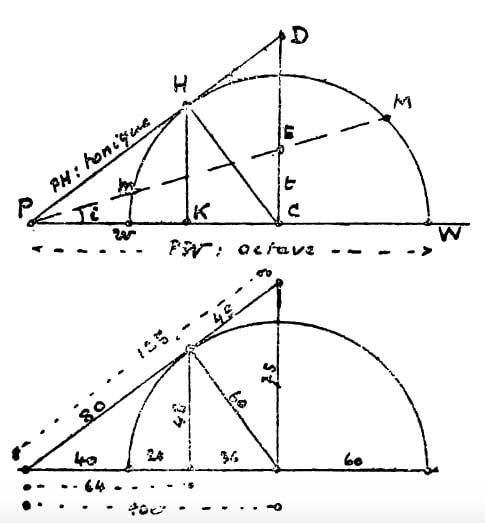
In the reproduction of this image in my translation, I have not only translated the indications in French, but also substituted 0 for C, and L for D, to avoid any confusion with C and D as names of musical notes in English. For dealing with the problem that I am going to expose here, I have also added some lines and letters in red ink:

On p. 91-2, the author gives a series of measurements of segments of that figure, assuming that PH = 1; PW = 2, and PW x Pw = 2 (2 – wW) = 1. Then, Pw = PW – wW = 2 – wW; PW x Pw = 2 (2 – wW) = 1; 4 – 2wW = 1; 4 – 1 = 2wW; 3 = 2wW; wW = 3/2. So, 0H = (wW)/2 = (3/2)/2 = 3/4, and P0 = √(1+9/16)=5/4.

Here we have the values of all the lengths of the above construction:

PH = h (base).

0H = radius of the circle = (3/4)h.

P0 = (5/4)h.

PW = 2h.

Pw = (1/2)h, since \( Pw=P0-wW/2=5/4-3/4=1/2 \)

PK = (4/5)h. For checking this, we must find PK, such that PK + K0 = P0 = 5/4, being 0H = 3/4, and PH = 1. Then, we shall have:
a) \[ (PK+K0)^2=〖PH〗^2+〖0H〗^2↔〖PK〗^2+2PK∙K0+〖K0〗^2=(5/4)^2=25/16 \]
b) On the other hand, according to the theorem of the cathetus being proportional mean between the hypotenuse and the projection of the cathetus on the hypotenuse, H0 is proportional mean between P0 and K0, that is: \[ H0/P0=K0/H0 \]
c) Now, since we know that P0 = 5/4, and H0 = 3/4, we may find K0: \[ (3/4)/(5/4)=K0/(3/4)↔K0=(3/4)^2/(5/4)=(9/16)/(5/4)=36/80=9/20 \]
d) And last, since PK + K0 = P0 = 5/4, PK + (9/20) = 5/4; PK = (5/4) – (9/20) = (25/20) – (9/20) = 16/20 = 4/5.

HK = (3/5)h. We already know that PK = 4/5 and PH = 1. Then, 1 = (4/5)2 + HK2, and \[ HK=√(1-(4/5)^2 )=√(25/25-16/25)=√(9/25)=3/5 \]

K0 = (9/20)h, as we saw in connection with PK.

0L = (15/16)h. We must find 0L, such that \[ 〖PL〗^2=〖0L〗^2+〖P0〗^2 \], where we only know that P0 = 5/4; but, on the other hand:
a) We know PH = 1, and PL = PH + HL = 1 + HL, so that\[ 〖PL〗^2=〖0L〗^2+〖P0〗^2↔(1+HL)^2=〖0L〗^2+(5/4)^2 \]
b) We know that P0 = 5/4, is proportional mean between the hypotenuse (PL, unknown) and the projection of P0 on the hypotenuse (PH = 1), so that
\[ P0/PL=PH/P0↔(5/4)/PL=1/(5/4)↔5/4=PL/(5/4)↔PL=25/16 \],
and, since
\[ PL=PH+HL \],
\[ 25/16=1+HL↔HL=25/16-1=9/16 \]
c) Now we must find 0L, by means of the theorem of Pythagoras:
\[ 〖PL〗^2=〖P0〗^2+〖0L〗^2↔(25/16)^2=25/16+〖0L〗^2↔〖0L〗^2=(25/16)^2-25/16=625/256-25/16=(625-400)/256=225/256↔0L=√(225/256)=15/16 \]

HL = (9/16)h, as we saw above.

0L / P0 is the tangent of the angle P: 0L / P0 = (15/16) / (5/4) = 60 / 80 = 3/4.

t = [(5/4)h] · tan i

Then, on p. 93, the author says that the ratio \[ PM/PH \] can be expressed by the formula \[ 5±√(9-16(tan⁡i )^2 )/(4√(1+(tan⁡i )^2 )) \], but he does not demonstrate it. This is my problem. I would like to demonstrate that myself, but I have not been able to do that so far.

I have thought that I must express PM and PH as functions of tan i:

a) I think it is not too complicated to express PM as a function of tan i. Let us remember how I completed the figure as a helping device:

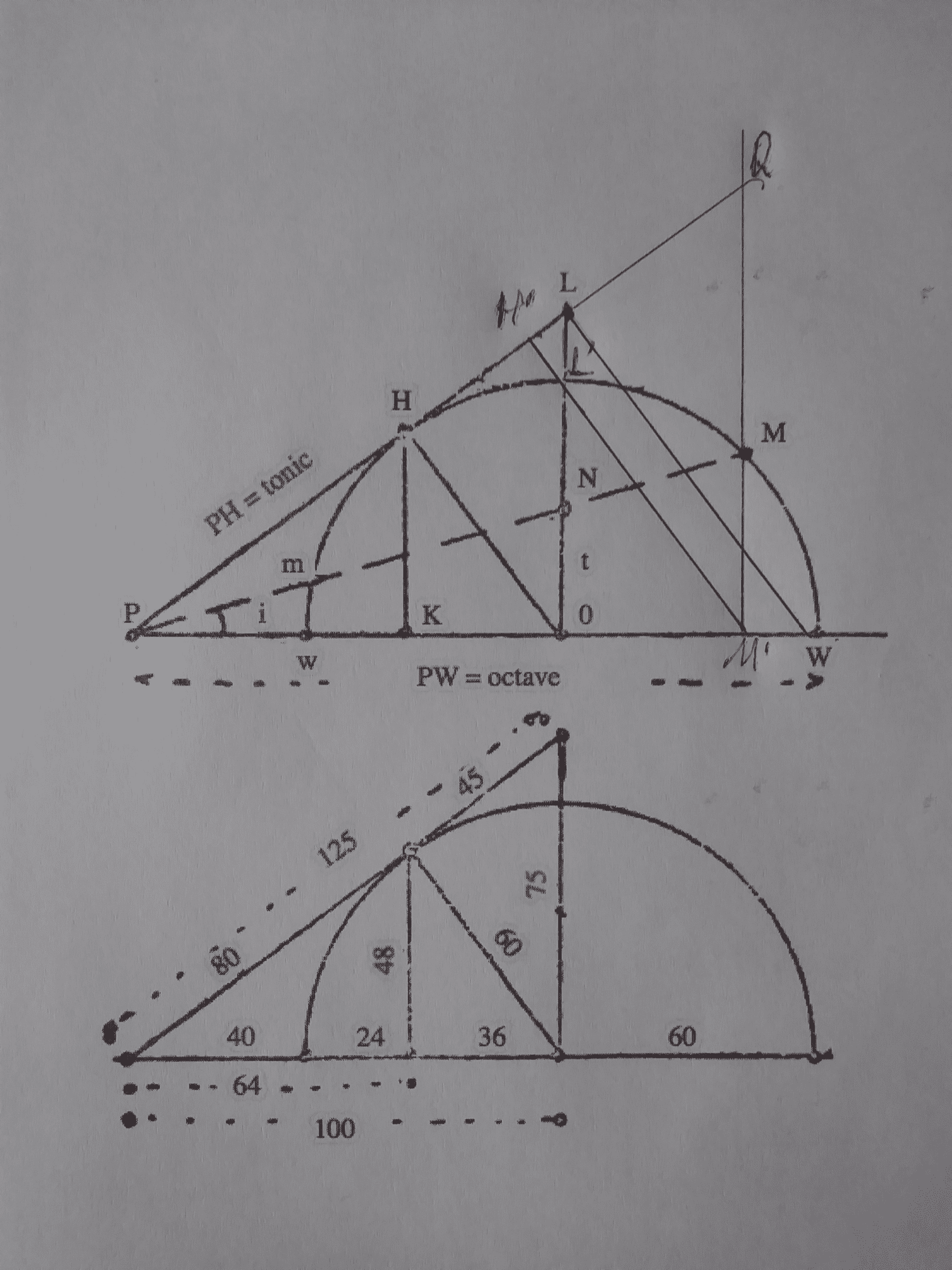
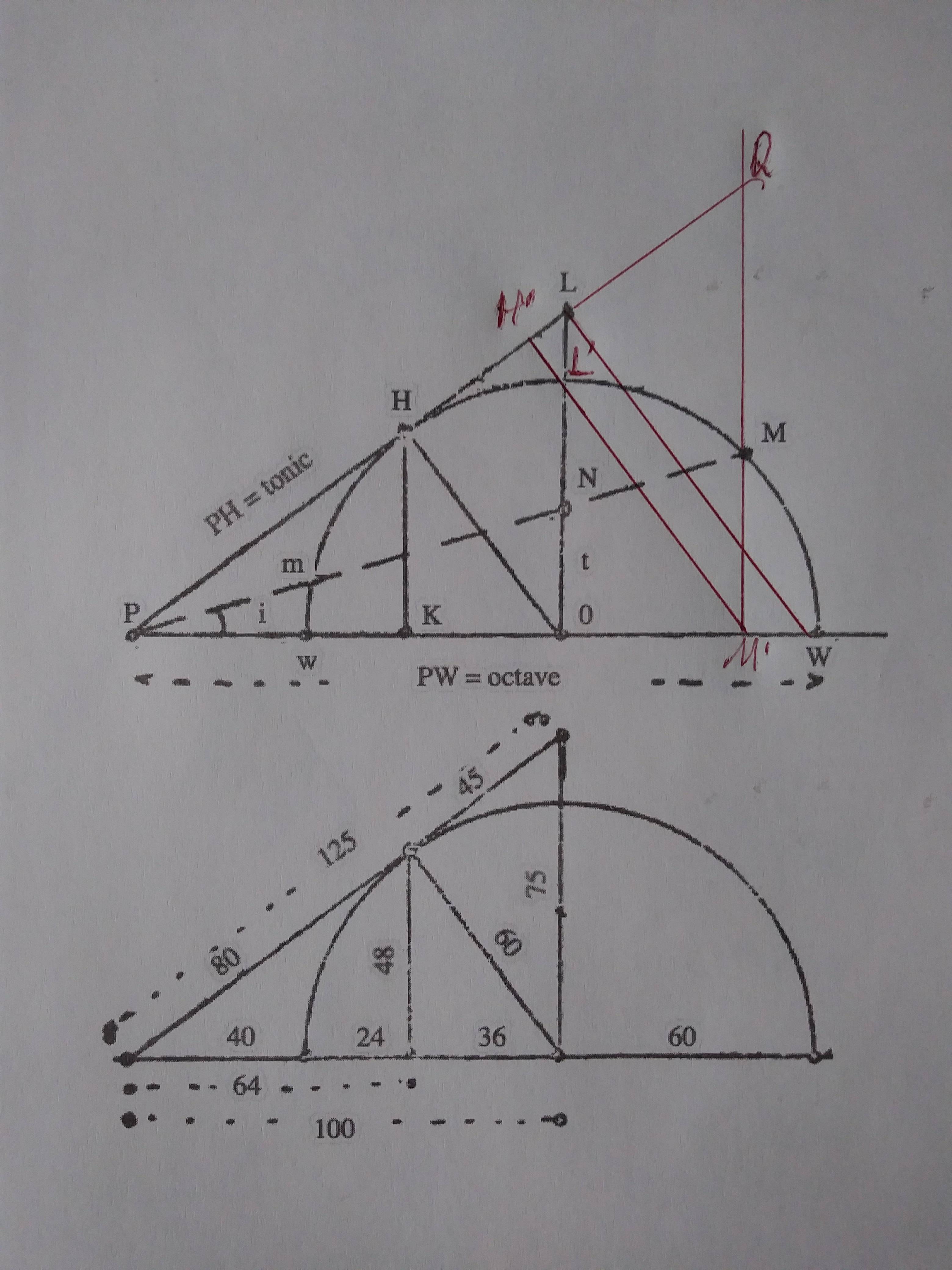
For expressing PM as a function of tan i, taking into account that \[ tan⁡i=MM'/PM' \], I have done this:
\[ tan⁡i=MM'/PM'↔MM^'=PM^'∙tan⁡i; 〖PM〗^2=(PM^'∙tan⁡i )^2+〖PM^'〗^2=〖PM^'〗^2 [1+(tan⁡i )^2 ]↔PM=√(〖PM^'〗^2 [1+(tan⁡i )^2 ] )=PM'√([1+(tan⁡i )^2 ] ) \]

b) For expressing PH as a function of tan i, I have noticed that, if we draw a perpendicular to PL, passing by the point in which 0L cuts the semi-circumference of our figure, and we lengthen it until it cuts the segment wW, we obtain the point M’ of the segments PM’ and MM’ with which we operated in the previous section. This may help us, as we shall see later.
On the other hand, there are two triangles, PH’M’ and PLW, which are similar to PH0.
We know the dimensions of PH0: PH = 1; 0H = 3/4, and P0 = 5/4.
On the other hand, 0H = 0w = 0W, so that PW = P0 + 0w = P0 + 0H = (5/4) + (3/4) = 8/4 = 2. This may help to find LW, since \[ P0/PW=H0/LW↔(5/4)/2=(3/4)/LW↔(LW∙5/4)/2=3/4↔LW∙5/4=2∙3/4=6/4↔LW=(6/4)/(5/4)=24/20=6/5 \]
Now we must find 0L. The triangles PHK and PL0 being similar,
\[ PK/P0=HK/0L↔(4/5)/(5/4)=(3/5)/0L↔16/25=(3/5)/0L↔16/25∙0L=3/5↔0L=(3/5)/(16/25)=75/80=15/16 \]
Now, knowing that 0L = 15/16, that 0L’ = 0H = 0W = 3/4, and that the triangles W0L and M’0L’ are similar, we may determine 0M’:
\[ 0L'/0L=0M'/0W↔(3/4)/(15/16)=0M'/(3/4)↔0M^'=(9/16)/(15/16)=144/240=3/5 \]
Our next step may be to determine MM’. We already know 0M’ = 3/5, and 0M = 0H = 0W = 3/4. So, according to the theorem of Pythagoras:
\[ 〖0M〗^2=〖0M'〗^2+〖MM'〗^2↔MM^'=√(〖0M〗^2-〖0M'〗^2 )=√((3/4)^2-(3/5)^2 )=√(9/16-9/25)=√((225-144)/400)=√(81/400)=9/20 \]
Now, once we know PM’, we must find the values of the other cathetus and of the hypotenuse of PM’Q, similar to PHK and to P0L. PQ is a prolongation of PH, and QM’ = QM + MM’. So:
\[ PK/PM'=HK/QM'↔(4/5)/(P0+0M')=(3/5)/QM'↔(4/5)/(5/4+3/5)=(3/5)/QM'↔(4/5)/((25+12)/20)=(3/5)/QM'↔(4/5)/(37/20)=(3/5)/QM'↔80/185=(3/5)/QM'↔QM^'∙80/185=3/5↔QM^'=(3/5)/(80/185)=555/400=111/80 \]
We must still find the value of PQ:
\[ PH/PQ=PK/PM'↔1/PQ=(4/5)/(37/20)↔1=PQ∙(4/5)/(37/20)↔PQ=(37/20)/(4/5)=185/80=37/16 \]

Before we proceed, we may sum up:
a) First, PH = 1; PQ = (37/16); PM’ = (37/20); MM’ = 9/20, and QM’ = 111/80. Thence, we may already deduce that PQ – PH = (37/16) – (16/16) = (21/16), that is, PQ = 1 + (21/16).
b) On the other hand, \[ tan⁡i=(MM^')/(PM^' )↔PM^'=(MM^')/tan⁡i "y " MM^'=PM'∙tan⁡i \]
c) QM’ = (111/80), and MM’ = (9/20), so that QM’ = (9/20) + QM, that is, QM = (111/80) – (9/20) = (111/80) – (36/80) = (75/80), or QM’ = [(75/80) + MM’] = [(75/80) + (PM’ x tan i)].

Now, taking all that into consideration, and according to the theorem of Pythagoras:
\[ 〖PQ〗^2=〖PM'〗^2+〖QM'〗^2↔(PH+21/16)^2=(MM'/tan⁡i )^2+[75/80+(PM'∙tan⁡i )]^2↔[〖PH〗^2+(2∙21/16∙PH)+(21/16)^2 ]=(MM'/tan⁡i )^2+[(75/80)^2+(2∙75/80∙PM'∙tan⁡i )+〖PM'〗^2∙(tan⁡i )^2 ]↔〖PH〗^2+42/16 PH+[(21/16)^2-((MM^')/tan⁡i )^2-(75/80)^2-(2∙75/80∙PM^'∙tan⁡i )-(PM'∙tan⁡i )^2 ]=0↔〖PH〗^2+42/16 PH+[441/256-5625/6400-((MM^')/tan⁡i )^2-(2∙75/80∙PM^'∙tan⁡i )-(PM'∙tan⁡i )^2 ]=0↔〖PH〗^2+42/16 PH+[(11025-5625)/6400-〖MM^'〗^2/(tan⁡i )^2 -(2∙75/80∙PM^'∙tan⁡i )-(PM'∙tan⁡i )^2 ]=0↔〖PH〗^2+42/16 PH+[5400/6400-(〖MM^'〗^2-(2∙75/80∙PM^'∙{tan⁡i }^3 )-PM'∙(tan⁡i )^4)/(tan⁡i )^2 ]=0 \]

Now we may do as follows:
\[ 〖PH〗^2+42/16 PH+[5400/6400-(〖MM^'〗^2-(2∙75/80∙PM^'∙{tan⁡i }^3 )-PM'∙(tan⁡i )^4)/(tan⁡i )^2 ]=0↔〖PH〗^2+42/16 PH+[5400/6400-({〖PM'〗^2∙(tan⁡i )^2 }-PM'∙({150/80∙[tan⁡i ]^3 }+{tan⁡i }^4 ))/(tan⁡i )^2 ]=0↔〖PH〗^2+42/16 PH+[5400/6400-({PM'∙(tan⁡i )^2 }∙{PM^'-(150/80∙tan⁡i )-〖tan⁡i〗^2 })/(tan⁡i )^2 ]=0↔〖PH〗^2+42/16 PH+({5400∙(tan⁡i )^2 }-6400∙{PM'∙(tan⁡i )^2 }∙{PM^'-(150/80∙tan⁡i )-〖tan⁡i〗^2 })/(6400∙(tan⁡i )^2 )=0↔PH=(-42/16±√((42/16)^2-4∙[({5400∙(tan⁡i )^2 }-6400∙{PM'∙(tan⁡i )^2 }∙{PM^'-(150/80∙tan⁡i )-〖tan⁡i〗^2 })/(6400∙(tan⁡i )^2 )] ))/2 \]

There we have PH expressed as a function of tan i and PM’. If we remember that \[ PM = PM'√([1+(tan⁡i )^2 ] ) \], we may write:
\[ PM/PH=(PM'√([1+(tan⁡i )^2 ] ))/((-42/16±√((42/16)^2-4∙[({5400∙(tan⁡i )^2 }-6400∙{PM'∙(tan⁡i )^2 }∙{PM^'-(150/80∙tan⁡i )-〖tan⁡i〗^2 })/(6400∙(tan⁡i )^2 )] ))/2)=(2∙PM'∙√([1+(tan⁡i )^2 ] ))/(-42/16±√((42/16)^2-4∙[({5400∙(tan⁡i )^2 }-6400∙{PM'∙(tan⁡i )^2 }∙{PM^'-(150/80∙tan⁡i )-〖tan⁡i〗^2 })/(6400∙(tan⁡i )^2 )] )) \]

But I cannot see how to simplify that monstrous equation to obtain \[ PM/PH=5±√(9-16(tan⁡i )^2 )/(4√(1+(tan⁡i )^2 )) \]

Thank you very much in advance for whatever help in detecting any wrong assumptions or calculations, and in the demonstration of that formula.

All best!

 

[Opalg]

The way to find $PM$ is to use the triangle $PMO$. In that triangle, you know that $PO$ is $\frac54h$, $OM$ is the radius of the semicircle, which is $\frac34h$, and the angle at $P$ is $i$. Stripping out all the other lines in the diagram and writing $PM = x$, the picture looks like this:
[TIKZ]\coordinate [label=left:$P$] (P) at (-6.7,0) ;
\coordinate [label=below:$O$] (O) at (0,0) ;
\coordinate [label=above right:$M$] (M) at (40:4) ;
\coordinate [label=above:$H$] (H) at (127:4) ;
\draw (4,0) arc (0:180:4) ;
\draw (5,0) -- (P) -- node[ above ]{$x$} (M) -- node[ below ]{$\frac34h$} (O) ;
\draw (P) -- node[ above ]{$h$} (H) ;
\draw (-5.5,0) arc (0:15:1.2) ;
\draw (-5.3,0.2) node{$i$} ;
\draw (-3,-0.3) node{$\frac54h$} ;
\draw (-4.2,0.9) node{$m$} ;[/TIKZ]
Now use the cosine rule in the triangle. This says that $OM^2 = OP^2 + PM^2 - 2 OP*PM*\cos i$, or $$\tfrac9{16}h^2 = \tfrac{25}{16}h^2 + x^2 - \tfrac52hx\cos i.$$ Divide through by $h^2$ and rearrange the equation to get $$\left(\tfrac xh\right)^2 - \tfrac52\cos i\left(\tfrac xh\right) + 1 = 0.$$ That is a quadratic equation for $\frac xh$, with solutions $$\frac xh = \frac14\left(5\cos i \pm\sqrt{25\cos^2 i - 16}\right).$$ More precisely, if you take the $+$ sign in that formula it gives you the ratio $\dfrac{PM}{PH}$, and if you take the $-$ sign it gives you the ratio $\dfrac{Pm}{PH}$.

That formula looks different from the formula $$\frac xh = \frac{5\pm\sqrt{9 - 16 \tan^2i}}{4\sqrt{1+\tan^2i}}$$ that you quote from the book. But in fact the two formulas are equivalent. To see that, use the fact that $\cos i = \dfrac1{\sqrt{1+\tan^2 i}}$ (which follows from the fact that $\cos^2i + \sin^2i = 1$).

 

[Kobzar]

The way to find $PM$ is to use the triangle $PMO$. In that triangle, you know that $PO$ is $\frac54h$, $OM$ is the radius of the semicircle, which is $\frac34h$, and the angle at $P$ is $i$. Stripping out all the other lines in the diagram and writing $PM = x$, the picture looks like this:
[TIKZ]\coordinate [label=left:$P$] (P) at (-6.7,0) ;
\coordinate [label=below:$O$] (O) at (0,0) ;
\coordinate [label=above right:$M$] (M) at (40:4) ;
\coordinate [label=above:$H$] (H) at (127:4) ;
\draw (4,0) arc (0:180:4) ;
\draw (5,0) -- (P) -- node[ above ]{$x$} (M) -- node[ below ]{$\frac34h$} (O) ;
\draw (P) -- node[ above ]{$h$} (H) ;
\draw (-5.5,0) arc (0:15:1.2) ;
\draw (-5.3,0.2) node{$i$} ;
\draw (-3,-0.3) node{$\frac54h$} ;
\draw (-4.2,0.9) node{$m$} ;[/TIKZ]
Now use the cosine rule in the triangle. This says that $OM^2 = OP^2 + PM^2 - 2 OP*PM*\cos i$, or $$\tfrac9{16}h^2 = \tfrac{25}{16}h^2 + x^2 - \tfrac52hx\cos i.$$ Divide through by $h^2$ and rearrange the equation to get $$\left(\tfrac xh\right)^2 - \tfrac52\cos i\left(\tfrac xh\right) + 1 = 0.$$ That is a quadratic equation for $\frac xh$, with solutions $$\frac xh = \frac14\left(5\cos i \pm\sqrt{25\cos^2 i - 16}\right).$$ More precisely, if you take the $+$ sign in that formula it gives you the ratio $\dfrac{PM}{PH}$, and if you take the $-$ sign it gives you the ratio $\dfrac{Pm}{PH}$.

That formula looks different from the formula $$\frac xh = \frac{5\pm\sqrt{9 - 16 \tan^2i}}{4\sqrt{1+\tan^2i}}$$ that you quote from the book. But in fact the two formulas are equivalent. To see that, use the fact that $\cos i = \dfrac1{\sqrt{1+\tan^2 i}}$ (which follows from the fact that $\cos^2i + \sin^2i = 1$).

Dear Opalg, thank you very much for your helpful answer. I did not know the cosine rule, which I am studying right now (the name for this is "lifelong learning"). But otherwise I have been able to follow your steps and obtain the proof for the formula.
Best regards.