John112
- 19
- 0
since the maclaurin series for sin x is alternating in sign (EQ1) so when you square it to get sin^{2}(x) (EQ2) the (-1)^{n} should become (-1)^{2n} (EQ3) which can be simplified down to (EQ4), but when i checked that series at wolframalpha the series was still alternating like: Why is that? So when we square it do we ignore squaring the (-1)^{n} and put that after we're done squaring the series?In the above post when I say EQ#, I'm referring to these equations
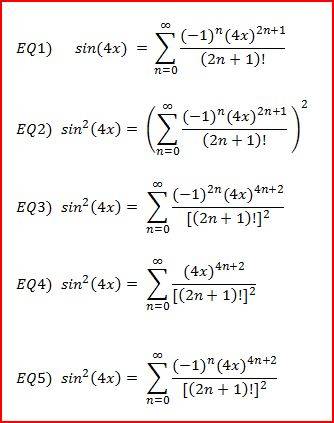
Last edited by a moderator: