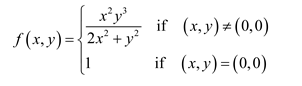I'll have an attempt at this problem now, most likely for future readers. I will first prove that the limit exists by using two methods, the first being an epsilon delta proof and the second with squeeze theorem. Then, since we find that the limit at the origin does not equal to value of the function, it does not satisfy the conditions of being continuous at the origin.
The squeeze theorem is quite straightforward to apply most of the time using the property $x^2\le x^2+y^2$ or $y^2\le x^2+y^2$.
We have $$\lim_{{(x,y)}\to{(0,0)}}\frac{x^2y^3}{2x^2+y^2}$$, and we can deduce the following:
$$0\le \left| \frac{x^2y^3}{2x^2+y^2} \right|< \frac{x^2\left| y^3 \right|}{x^2+y^2} \le \frac{(x^2+y^2)\left| y^3 \right|}{x^2+y^2}=\left| y^3 \right|$$
As we take the limit as $(x,y)$ tends to $(0,0)$ on the right most inequality, by the squeeze theorem, $$\lim_{{(x,y)}\to{(0,0)}}\frac{x^2y^3}{2x^2+y^2}$$ must also equal zero. From here, we can say that the given piecewise function is not continuous at $(0,0)$Alternatively, we can use an epsilon delta proof.
For all $\epsilon>0$, there exists a $\delta$ such that whenever $\left| \text{x}-\text{a} \right|<\delta$, $\left| f(\text{x})-L \right|<\epsilon$, where $\text{x}=(x,y), \text{a}=(a,b)$, both vectors. In other words, whenever $\sqrt{(x-a)^2+(y-b)^2}<\delta, \left| f(x,y)-L \right|<\epsilon$.
In this problem, we have $\sqrt{x^2+y^2}<\delta$, $$\left| \frac{x^2y^3}{2x^2+y^2} \right|<\epsilon$$.
From above, we have shown that $$\left| \frac{x^2y^3}{2x^2+y^2} \right|<\left| y \right|^3=\left(x^2+y^2\right)^{3/2}$$. Set $\delta = \epsilon ^{1/3}$. So for any $\epsilon$, we have:
$\sqrt{x^2+y^2}<\delta =\epsilon ^{1/3}$
$(x^2+y^2)^{3/2}<\epsilon$
$$\frac{x^2y^3}{2x^2+y^2} <\epsilon$$, as required.
The limit exists and equals $0$, which is not equal to the function evaluated at $(0,0)$, therefore the function is not continuous at the origin.