How can we improve the estimate?

[evinda]

Hello! (Wave)

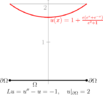
Let $u(x)$ be a solution of the problem

$$Lu=-1 \text{ in } \Omega , u|_{\partial{\Omega}}=2, (c(x) \leq 0)$$

I want to determine the constants $c_1,c_2$ such that $c_1 \leq u(x) \leq c_2 (1)$.

Also I want to improve the estimate $(1)$ when it is furthermore given that $c(x) \equiv -1$.

I thought to use the following lemma:

Let $L$ be an elliptic operator in a bounded space $\Omega$ and $u \in C^2(\Omega) \cup C^0(\overline{\Omega})$.
If $Lu \geq 0 (\leq 0) \ \ \ \ \ \ c \leq 0 \text{ in } \Omega$
then $$\sup_{\Omega} u \leq \max \left( \sup_{\partial{\Omega}} u, 0\right) \\ \left( \inf_{\Omega} u \geq \min \{ \inf_{\partial{\Omega}} u, 0\} \right)$$

From this, if we consider that $\Omega$ is bounded , we get that $\inf_{\Omega} u \geq 0$ and so $u \geq 0$.

For the other inequality, I thought to use the following theorem:

Let $Lu=f$ in a bounded space $\Omega$, where $L$ is an elliptic operator and $u \in C^2(\Omega) \cap C^0(\overline{\Omega})$. Then $$\sup_{\overline{\Omega}} |u| \leq \sup_{\partial{\Omega}} |u|+ C \sup \frac{|f|}{\lambda}$$

where $C=e^{\alpha d}-1 $

($d $: $ \Omega \subset \{ 0< x_1< d\}$)

($\alpha \geq \frac{\sup{|\beta_1|}}{\lambda}+1$)

($\beta_1: Lu= \sum_{i,j=1}^n a_{ij} u_{x_i x_j}+ \sum_{i=1}^n \beta_i u_{x_i}+cu $ )

($\lambda: 0< \lambda |\xi|^2 \leq \sum_{i,j=1}^n a_{ij} \xi_i \xi_j \ \ \ \ \xi \in \mathbb{R}^n, x \in \Omega $)

From this get that $ \sup_{\overline{\Omega}} |u| \leq 2+ \frac{C}{\lambda} $, so $u \leq 2+\frac{C}{\lambda}$.

Is it right so far? How can we improve the estimate $0 \leq u(x) \leq 2+ \frac{C}{\lambda} $ when we know furthermore that $c(x) \equiv -1$ ? (Thinking)

 

[I like Serena]

Hey evinda! (Smile)

Looks right to me.

Btw, didn't we have:

We have the following theorem:

Theorem: We suppose that $u \in C^2(\Omega)$ satisfies in the space $\Omega$ the relation $Lu \geq 0$ ($Lu \leq 0$). We suppose that $\Omega$ satisfies the interior sphere condition.
If $c \leq 0$ then $u(x)$ does not achieve its positive maximum in $\Omega$, i.e. in $\overline{\Omega} \setminus{\partial{\Omega}}$ (negative minimum) if it is not constant.
If $c \equiv 0$ then $u$ does not achieve its maximum in $\Omega$ (minimum) if it is not constant.

Couldn't we find a better estimate with it? (Wondering)

 

[evinda]

Btw, didn't we have:Couldn't we find a better estimate with it? (Wondering)

I thought that we cannot use it since we have $Lu \leq 0$ and $u|_{\partial{\Omega}}=2$ and so we don't have a negative minimum. Do you agree? (Thinking)

 

[I like Serena]

I thought that we cannot use it since we have $Lu \leq 0$ and $u|_{\partial{\Omega}}=2$ and so we don't have a negative minimum. Do you agree? (Thinking)

Indeed, we can't use it. (Blush)

 

[evinda]

Indeed, we can't use it. (Blush)

(Smile)

Do you have an idea how we can find a better estimate,when we assume that $c(x) \equiv -1$ ?

 

[I like Serena]

(Smile)

Do you have an idea how we can find a better estimate,when we assume that $c(x) \equiv -1$ ?

Repeating your idea from your previous thread... (Thinking)

Suppose $u$ has a maximum at $x_0 \in \overline\Omega$ (assuming that $\Omega$ is bounded).
Then:
$$Lu(x_0)= \sum_{i,j=1}^n a_{ij} u_{x_i x_j}+cu(x_0) = -1 \quad\Rightarrow\quad c(x_0)u(x_0) \ge -1
\quad\Rightarrow\quad u(x_0) \le \frac{-1}{c(x_0)}$$
For $c(x_0)=-1$ this becomes:
$$u(x) \le u(x_0) \le 1$$
(Happy)

 

[evinda]

Repeating your idea from your previous thread... (Thinking)

Suppose $u$ has a maximum at $x_0 \in \overline\Omega$ (assuming that $\Omega$ is bounded).
Then:
$$Lu(x_0)= \sum_{i,j=1}^n a_{ij} u_{x_i x_j}+cu(x_0) = -1 \quad\Rightarrow\quad c(x_0)u(x_0) \ge -1
\quad\Rightarrow\quad u(x_0) \le \frac{-1}{c(x_0)}$$
For $c(x_0)=-1$ this becomes:
$$u(x) \le u(x_0) \le 1$$
(Happy)

In the same way, suppose that $u$ has a minimum at $x_1 \in \overline\Omega$ .
Then:

$$Lu(x_1)= \sum_{i,j=1}^n a_{ij}(x_1) u_{x_i x_j}(x_1)+cu(x_1) = -1 \quad\Rightarrow\quad c(x_1)u(x_1) \le -1
\quad\Rightarrow\quad u(x_1) \ge \frac{-1}{c(x_1)}$$
For $c(x_1)=-1$ this becomes:
$$u(x) \ge u(x_1) \ge 1$$

So, when $c \equiv -1$, the solution of the problem is $u=1$, right? (Thinking)

 

[I like Serena]

In the same way, suppose that $u$ has a minimum at $x_1 \in \overline\Omega$ .
Then:

$$Lu(x_1)= \sum_{i,j=1}^n a_{ij}(x_1) u_{x_i x_j}(x_1)+cu(x_1) = -1 \quad\Rightarrow\quad c(x_1)u(x_1) \le -1
\quad\Rightarrow\quad u(x_1) \ge \frac{-1}{c(x_1)}$$
For $c(x_1)=-1$ this becomes:
$$u(x) \ge u(x_1) \ge 1$$

So, when $c \equiv -1$, the solution of the problem is $u=1$, right? (Thinking)

Hmm... suppose we pick... an example! (Wait)
View attachment 6207

I'm not sure if the solution $u=1$ is correct. (Worried)

 

[evinda]

Why was my argumentation with the minimum value wrong? (Thinking)Also can a function that is smaller or equal to $1$ be equal to $2$ at the boundary? (Sweating)

 

[I like Serena]

Why was my argumentation with the minimum value wrong? (Thinking)Also can a function that is smaller or equal to $1$ be equal to $2$ at the boundary? (Sweating)

We assumed that u had a maximum where the derivative was zero. I think we have proven that there is no internal maximum when c=-1. Instead we have the sharper boundary maximum of 2! (Smile)

 

[evinda]

We assumed that u had a maximum where the derivative was zero. I think we have proven that there is no internal maximum when c=-1. Instead we have the sharper boundary maximum of 2! (Smile)

We have that if $c<0, Lu \leq 0$ or $c \leq 0, Lu<0$ then $u$ does not achieve its negative minimum at the internal points of $\Omega$.

If we have the condition $c <0, Lu \geq 0$ or $c \leq 0, Lu>0$ we can deduce that the positive maximum is not achieved at the internal points of $\Omega$.

 

[I like Serena]

We have that if $c<0, Lu \leq 0$ or $c \leq 0, Lu<0$ then $u$ does not achieve its negative minimum at the internal points of $\Omega$.

If we have the condition $c <0, Lu \geq 0$ or $c \leq 0, Lu>0$ we can deduce that the positive maximum is not achieved at the internal points of $\Omega$.

Yes. And we can apply neither here.

Instead we assumed there was an internal maximum, and found an upper boundary of $1$, which is a contradiction, since we have boundary values of $2$.
Therefore the assumption should be false: there is no internal maximum.
Shouldn't it? (Thinking)

 

[evinda]

Yes. And we can apply neither here.

Instead we assumed there was an internal maximum, and found an upper boundary of $1$, which is a contradiction, since we have boundary values of $2$.
Therefore the assumption should be false: there is no internal maximum.
Shouldn't it? (Thinking)

Yes, it should. So from this we deduce that the maximum is achieved at the boundary, and so $u(x) \leq 2$, right? (Thinking)
From this:

In the same way, suppose that $u$ has a minimum at $x_1 \in \overline\Omega$ .
Then:

$$Lu(x_1)= \sum_{i,j=1}^n a_{ij}(x_1) u_{x_i x_j}(x_1)+cu(x_1) = -1 \quad\Rightarrow\quad c(x_1)u(x_1) \le -1
\quad\Rightarrow\quad u(x_1) \ge \frac{-1}{c(x_1)}$$
For $c(x_1)=-1$ this becomes:
$$u(x) \ge u(x_1) \ge 1$$

we don't get a contradiction, do we?
The boundary value is $2$ and if the minimum is achieved at an internal point, let $x_1$ , we have that $u(x_1) \geq 1$.

So $1$ is the minimum value of $u$, right?

 

[I like Serena]

Yes, it should. So from this we deduce that the maximum is achieved at the boundary, and so $u(x) \leq 2$, right? (Thinking)

From this:

we don't get a contradiction, do we?
The boundary value is $2$ and if the minimum is achieved at an internal point, let $x_1$ , we have that $u(x_1) \geq 1$.

So $1$ is the minimum value of $u$, right?

Right. (Nod)

I do believe we should assume $x_1 \in \Omega\setminus \partial\Omega$, because we require the derivatives to be zero, which is not necessarily the case if the minimum is on the boundary, but the derivatives have to be zero if it's an internal minimum.
Furthermore, we should also consider that the minimum may be on the boundary, in which case it is $2$.
Since $1$ is less than $2$, we can conclude we have a lower estimate of $1$. (Thinking)

 

[evinda]

Right. (Nod)

I do believe we should assume $x_1 \in \Omega\setminus \partial\Omega$, because we require the derivatives to be zero, which is not necessarily the case if the minimum is on the boundary, but the derivatives have to be zero if it's an internal minimum.
Furthermore, we should also consider that the minimum may be on the boundary, in which case it is $2$.
Since $1$ is less than $2$, we can conlude we have a lower estimate of $1$. (Thinking)

We should also consider that $x_0 \in \Omega\setminus \partial\Omega$, right?

You mean that if we have the maximum at an internal point $x_0$, then $\frac{\partial{u}}{\partial{v}}(x_0)=0$, but if $x_0$ is on the boundary then it does not necessarily hold that $\frac{\partial{u}}{\partial{v}}(x_0)=0$ ?

 

[evinda]

Furthermore, we should also consider that the minimum may be on the boundary, in which case it is $2$.
Since $1$ is less than $2$, we can conlude we have a lower estimate of $1$. (Thinking)

Since $c \leq 0$, the function should have a negative minimum, so in this case it cannot be achieved at the boundary. Right? (Thinking)

 

[I like Serena]

We should also consider that $x_0 \in \Omega\setminus \partial\Omega$, right?

You mean that if we have the maximum at an internal point $x_0$, then $\frac{\partial{u}}{\partial{v}}(x_0)=0$, but if $x_0$ is on the boundary then it does not necessarily hold that $\frac{\partial{u}}{\partial{v}}(x_0)=0$ ?

Yes. (Nod)

Since $c \leq 0$, the function should have a negative minimum, so in this case it cannot be achieved at the boundary. Right? (Thinking)

How so?

We found that the internal minimum, if we have one for c=-1, has to be at least 1.
And indeed, in my example it's between 1 and 2. (Thinking)

 

[evinda]

How so?

We found that the internal minimum, if we have one for c=-1, has to be at least 1.
And indeed, in my example it's between 1 and 2. (Thinking)

I thought so because of the following lemma:

If $c<0, Lu \leq 0$ or $c \leq 0, Lu<0$ then $u$ cannot achieve its negative minimum at the internal points of $\Omega$.

So can it be that there is a positive minimum, that is achieved at the internal points of $\Omega$ ? (Thinking)

 

[I like Serena]

I thought so because of the following lemma:

If $c<0, Lu \leq 0$ or $c \leq 0, Lu<0$ then $u$ cannot achieve its negative minimum at the internal points of $\Omega$.

So can it be that there is a positive minimum, that is achieved at the internal points of $\Omega$ ? (Thinking)

Suppose we repeat your reasoning from before for these cases, don't we get that the internal minimum, if there is one, is at least 0? (Wondering)

So indeed, there can be no negative internal minimum, but still one that is at least zero. (Cool)

 

[evinda]

Suppose we repeat your reasoning from before for these cases, don't we get that the internal minimum, if there is one, is at least 0? (Wondering)

So indeed, there can be no negative internal minimum, but still one that is at least zero. (Cool)

You mean this one, right?

$$\inf_{\Omega} u \geq \min \{ \inf_{\partial{\Omega}} u, 0\}$$

 

[I like Serena]

You mean this one, right?

$$\inf_{\Omega} u \geq \min \{ \inf_{\partial{\Omega}} u, 0\}$$

That sums it up yes. (Mmm)

 

[evinda]

Nice... Thanks a lot! (Smirk)