Michio Cuckoo
- 84
- 0
Where
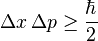
How did he come up with that?
How did he come up with that?
Heisenberg's uncertainty principle, articulated through the relation \(\Delta x \Delta p \ge \frac{\hbar}{2}\), was not derived in the traditional sense but rather conceptualized through thought experiments and later formalized by others using mathematical frameworks like Fourier analysis. The principle highlights the intrinsic limitations in measuring position and momentum simultaneously, independent of measurement apparatus. Historical context reveals that the development of quantum mechanics was influenced by earlier mathematical concepts and experimental evidence, particularly de Broglie's hypothesis regarding wave-particle duality. Schrödinger's wave equation, developed in parallel, further solidified the wave-like nature of particles.
PREREQUISITESStudents of physics, quantum mechanics researchers, and educators seeking to deepen their understanding of foundational principles in quantum theory.
Check out "The Physical Principles of the Quantum Theory". First published around 1935 I think.Michio Cuckoo said:Where
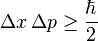
How did he come up with that?
bapowell said:The mathematical inequality actually follows from Fourier analysis.
This is an enlightening observation, imho. The Heisenberg uncertainty relations weren't just plucked from nothing. They have historical, mathematical basis. Heisenberg, like Einstein, Bohr, de Broglie, Jordan, Dirac, et al., was a genius of sorts, but not a magician. Everything to do with the development of the quantum theory has some basis in prior mathematics and classical conceptualization. Or so I like to believe.jtbell said:This means that a similar principle applies in other areas where we use Fourier analysis. For example, an electrical signal pulse contains a range of frequencies (or wavelengths) that is inversely proportional to the time duration or spatial width of the pulse. Likewise for pulses of electromagnetic radiation (e.g. light).
This has been known since probably sometime in the 1800s, so when physicists started to think of describing particles using waves, and superpositions of them, it was only a matter of time before someone applied this general uncertainty principle to QM.
Well, everyone "knew" that QM was about matter waves. Heisenberg was fiddling around with algebra of Hermitian operators that acted on physical states, but what was missing was a wave equation that actually described the evolution of these states. The impetus to develop a wave equation was largely driven by de Broglie's result and the experimental indications of the wave nature of matter.ThomasT said:and I don't really understand the basis for Schroedinger's wave equatiion.
Thanks bapowell. Every bit of input from certain perspectives helps. But I fear that I might be too old (and too lazy) to ever really understand this stuff.bapowell said:Well, everyone "knew" that QM was about matter waves. Heisenberg was fiddling around with algebra of Hermitian operators that acted on physical states, but what was missing was a wave equation that actually described the evolution of these states. The impetus to develop a wave equation was largely driven by de Broglie's result and the experimental indications of the wave nature of matter.
bapowell said:The impetus to develop a wave equation was largely driven by de Broglie's result and the experimental indications of the wave nature of matter.
emailanmol said:Isn't the relation dependent on the method we are using to find the variables (like x and v of electron?
Like on the microscope?
genericusrnme said:Nope, it is completely independent of any measuring apparatus although this is commonly used as a way to explain it for the case of the x-p uncertainty before we learn that they are a Fourier transform away from each other.
No matter what your measuring device you will never be able to tell its position and momentum exactly.
Take a dirac delta function (or a wave with one really big spike somewhere), you can tell where it is but you cannot tell it's frequency since it's just one spike. Similarly, take a uniform sine wave, you can tell it's frequency but you cannot tell where it is.
This is more the nature of the x-p uncertainty principle.
If, in the position basis we have a delta function (this just means we know its position exactly) we cannot gain any useful information about its momentum (we cannot tell it's frequency). If we have a delta function in the momentum basis (we know it's momentum exactly) we have a specific frequency (just like the uniform sine wave) and we cannot gain any information about its position.
We can get interesting little 'wave packets' where we can have some information about the position and some about the momentum, the gaussian wavepacket gives us the minimum uncertainty \sigma_x \sigma_p = \frac{\hbar}{2}
Also, going back to your superhuman eyes example, for these super human eyes to be able to give precice information about where the electron is, you need to bombard it with short and shorter wavelength photons which have higher and higher energies. If you bombard it with long wavelengthed photons, you won't disturb it much but you can essentially only know if the electron is in an area of size proportional to the wavelength of the photon.
emailanmol said:Oh.Now i get it.
The way they usually talk about in books, led me to think it was an apparatus dependent error.
Thanks a lot for clearing that up :-)