Warr
- 119
- 0
A projectile is ejected into an experimental fluid at time t = 0. The initial speed is v0 and the angle to the horizontal is theta. The drag in the projectile results in an acceleration term a_d=-kv, where k is a constant and v is the velocity of the projectile. Determine the x- and y-components of both the velocity and displacement as functions of time. What is the terminal velocity? Include the effects of gravitational acceleration.
here's a diagram:
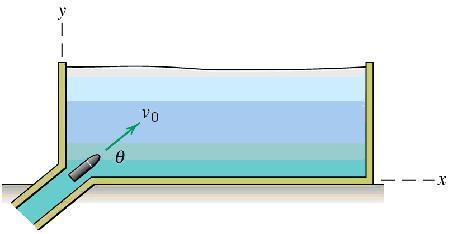
I don't really know what I'm doing here.
What I tried was splitting it into components and solving the dif eqs. I didn't know what 'constants' of integration would do so I just left them out.
a_x = -kv_x
v_x = e^(-kt)
a_y = -kv_y - g
v_y = -(gt)e^(-k*t)
let me just say I seriously do not know what I'm doing. Thus far we hadn't had any dif. eqs in the examples in class. No drag forces with gravity or anything. Btw this has to be solved with dynamics not statics I believe. I'm probably going in the completely wrong direction..
here's a diagram:
I don't really know what I'm doing here.
What I tried was splitting it into components and solving the dif eqs. I didn't know what 'constants' of integration would do so I just left them out.
a_x = -kv_x
v_x = e^(-kt)
a_y = -kv_y - g
v_y = -(gt)e^(-k*t)
let me just say I seriously do not know what I'm doing. Thus far we hadn't had any dif. eqs in the examples in class. No drag forces with gravity or anything. Btw this has to be solved with dynamics not statics I believe. I'm probably going in the completely wrong direction..
Attachments
Last edited: