riseofphoenix
- 294
- 2
8. A setup similar to the one shown in the figure below is often used in hospitals to support and apply a traction force to an injured leg.
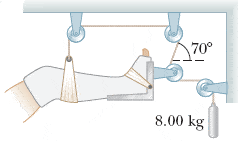
(a) Determine the force of tension in the rope supporting the leg.
F = mg
F = (8.00)(9.81)
F = 78.48
F = 78.5 N
Is that all I had to do? It says I got the answer for this part right.
(b) What is the traction force exerted on the leg? Assume the traction force is horizontal.
This is where I'm completely lost and confused.
First of all, the horizontal traction force they are referring to is the longest one on top right?
If so, then do I have to find the value of that horizontal line?
How?
They say the answer is supposed to be 105 N
Help!
(a) Determine the force of tension in the rope supporting the leg.
F = mg
F = (8.00)(9.81)
F = 78.48
F = 78.5 N
Is that all I had to do? It says I got the answer for this part right.
(b) What is the traction force exerted on the leg? Assume the traction force is horizontal.
This is where I'm completely lost and confused.
First of all, the horizontal traction force they are referring to is the longest one on top right?
If so, then do I have to find the value of that horizontal line?
How?
They say the answer is supposed to be 105 N
Help!
