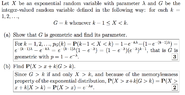How Do Probability Formulas for Bayes Theorem and Exponential Distribution Work?
- Context: MHB
- Thread starter Longines
- Start date
-
- Tags
- Parameters
Click For Summary
SUMMARY
This discussion focuses on the application of Bayes' Theorem and the Exponential Distribution in probability calculations. The first formula presented, $\displaystyle P \{ G = k\} = \int_{k-1}^{k} e^{- \lambda\ x}\ d x = e^{\lambda\ k} (e^{\lambda} - 1)$, illustrates the probability of a random variable G taking a specific value k. The second formula, $\displaystyle P\{X > k + x| G > k \} = e^{- \lambda\ x}$, demonstrates how to calculate conditional probabilities using Bayes' Theorem. Both formulas are essential for understanding probabilistic modeling in statistics.
PREREQUISITES- Understanding of Exponential Distribution
- Familiarity with Bayes' Theorem
- Basic calculus for integration
- Knowledge of probability theory
- Study the properties of Exponential Distribution in-depth
- Explore advanced applications of Bayes' Theorem in statistical inference
- Learn integration techniques relevant to probability calculations
- Investigate real-world examples of probabilistic modeling
Statisticians, data scientists, and anyone involved in probabilistic modeling or statistical analysis will benefit from this discussion.
Similar threads
- · Replies 31 ·
Graduate
Uncertainties on Bayes' theorem
- · Replies 19 ·
- · Replies 1 ·
- · Replies 1 ·
- · Replies 11 ·
- · Replies 5 ·
- · Replies 5 ·
- · Replies 5 ·
- · Replies 2 ·
- · Replies 24 ·