How Do You Calculate the Electrostatic Force Between Two Charged Lines?

[mousesgr]

Electricity and Magnetism urgent!pls!

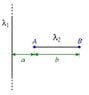
An infinite long line of charge of constant charge density a is located near the line AB which carries uniform charges with charge density b. Suppose both two lines are in the same plane, calculate the electrostatic force exerted on the line AB.

i don't know how to start...

 

[lightgrav]

Always start with a diagram, with labels
and a coordinate system. Label the items
described in the problems' situation,
and the quantity being asked about.

F=qE becomes F_vec = integral (dq E_vec).
Gauss says the infinitely-long charge density
carries a radial E-field that drops off as 1/r,
so unless AB is parallel to it, E=E(r).

If this sounds like gobbledy-gook, drop.
If this sounds like simple stuff you already knew,
the don't say "I don't know how to start".

 

[mousesgr]

the diagram

what is the limit of the integal then?
a to b or 0 to b?

 

[lightgrav]

you only need to integrate where the charges are ...
Your Diagram should include a dx (label it!)
and an E-field (presuming lamda_1 >0) at dx

F_on_dq = (dq)(E_at_dq)

If you integrate from 0 to A, use dq =0 there!
between A and B , dq = "b"dx .

 

[mousesgr]

you only need to integrate where the charges are ...
Your Diagram should include a dx (label it!)
and an E-field (presuming lamda_1 >0) at dx

F_on_dq = (dq)(E_at_dq)

If you integrate from 0 to A, use dq =0 there!
between A and B , dq = "b"dx .

what is the direction of dx & e-field then?

 

[lightgrav]

Come on! E-field due to the infinite line of charge
points _away_ from the positive charges there.

dx or dr is the coordinate (NOT vector) along line AB,
which is a geometric way of keeping track of the charges.
You're just adding F_vectors for each charge on AB ...
the total amount of charge on line AB is :
integral(dq) = integral(lamda_2 * dx) = lamda_2 * Length.

But don't expect F_total to be E(a+b/2) * lamda_2 * L !