How Do You Calculate Vector Change in 2D Elastic Billiard Ball Collisions?

[MatusVeselka]

Homework Statement

Hello I am trying to predict vector after collision of 2 ball in biliard. I am using angle-free representation formulas from wikipedia : https://wikimedia.org/api/rest_v1/media/math/render/svg/14d5feb68844edae9e31c9cb4a2197ee922e409cx1 and x2 are positions of balls, m1 and m2 are masses of balls, v1 and v2 are vectors of direction before collision and the angle brackets indicate the inner product (or dot product) of two vectors.

my values are :
x1 = (0.5 , 0)
x2 = (0 , 1)
m1,m2 = 1
v1 = (0.5, 1)
v2 = (0, 0)

Homework Equations

The Attempt at a Solution

[/B]
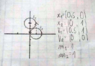
And here its my solution with vector (0.835 , 0.329), but this result can't be correct can somebody help me what I am doing wrong ? My result is total wrong and i don't know why

 

[BvU]

Hello Matus,

Who says it's totally wrong ?
As it happens, the wikipedia page has an animation of 2 5 SF pieces colliding in exactly ($\approx$) this way. You could take screen shots and measure the vectors !

 

[MatusVeselka]

When i simulate my example on some online calculators then vectors must look like this for my parameters

But my final vector after collision its going to wrong direction :(

 

[BvU]

some online calculators

Hogwash: there $\vec v_2\ne0$

 

[neilparker62]

Following might help - it presents a vector based technique for 2d collisions. Bit long winded but I think you get there in the end!

http://www.vobarian.com/collisions/2dcollisions2.pdf