- #1
Dandi Froind
- 7
- 0
Homework Statement
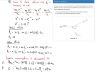
A billiard ball moves at a speed of 4.00m/s and collides elastically with an identical stationary ball. As a result, the stationary ball flies away at a speed of 1.69m/s, as shown in Figure A2.12. Determine:
- the final speed and direction of the incoming ball after the collision.
- the direction of the stationary ball after the collision.
Homework Equations
Conservation of Energy and momentum:
E before = E after
Σpx=0
Σpy=0
The Attempt at a Solution
As you can see, I have 2 equations with 2 angles that I don't know.
However, I couldn't find the right way to solve it due to trigonometry complexity.
I am sure that taking into account the fact that (sin(theta))^2 +(cos(theta))^2 = 1 would help in some way.
https://image.ibb.co/gv6YVw/Capture.jpg