Homework Help Overview
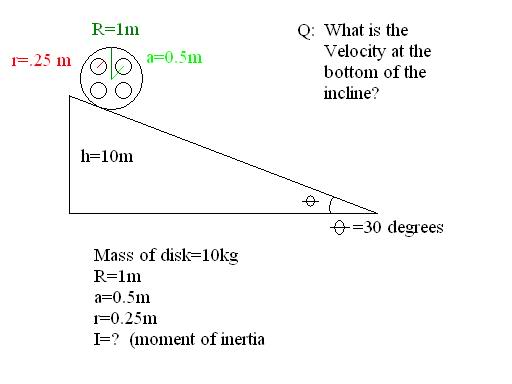
The discussion revolves around deriving the moment of inertia for a film projection wheel that has four holes in its center. Participants are exploring the implications of these holes on the overall moment of inertia, particularly in the context of rotational dynamics.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Assumption checking
Approaches and Questions Raised
- Participants discuss the addition of inertias for multiple masses and the concept of negative mass disks due to the holes. There is uncertainty about how to set up the integral for the moment of inertia and whether integration is necessary. Some participants suggest using known formulas for inertia, while others express confusion about applying the parallel axis theorem and how it relates to the holes.
Discussion Status
The discussion is active, with participants raising questions about the correct approach to account for the holes in the wheel. Some guidance has been provided regarding the use of the parallel axis theorem and the need to calculate moments of inertia for the holes, but there is still a lack of consensus on the best method to derive the final formula.
Contextual Notes
Participants are navigating through assumptions about mass distribution and the geometry of the wheel. There is mention of specific values, such as the mass of the disk being 10 kg, but the exact details of the setup and dimensions are not fully clarified.