How Do You Solve a 2D Elastic Collision Problem with Angle Relationships?

[chadarebubble]

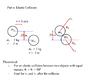
Homework Statement

The attached file is all the information on the problem

Homework Equations

.5mv^2 =.5mv1^2 + .5m2^2
p = mv

The Attempt at a Solution

I've tried plugging the known values in the equations and and substituting the various equations together and every time I come up with an equation that has two unknowns in it.

 

[kuruman]

Did you write down three (3) equations? Two for momentum conservation and one for energy conservation.

 

[chadarebubble]

Did you write down three (3) equations? Two for momentum conservation and one for energy conservation.

yes I did, the equations I was able to come up with are:
V₁cos(θ₁) + V₂cos(θ₂) = 5 (momentum in x direction)
V₁sin(θ₁) + V₂sin(θ₂) = 0 (momentum in y direction)
.5(V₁)² + .5(V₂)² = 12.5 (energy conservation)
θ₁ + θ₂ = 90

I worked on these equations for about an hour and came up with nothing, and feel like there is something I'm missing

 

[kuruman]

Sorry, I cannot read the fine print. Can you make all characters the same size?

 

[chadarebubble]

Sorry, I cannot read the fine print. Can you make all characters the same size?

Had a problem with subscripts overlapping but I think it's fixed.

 

[kuruman]

You are missing that sinθ₁ = cosθ₂ and cosθ₁ = sinθ₂. You should be able to get either one of these angles from the geometry of the collision.