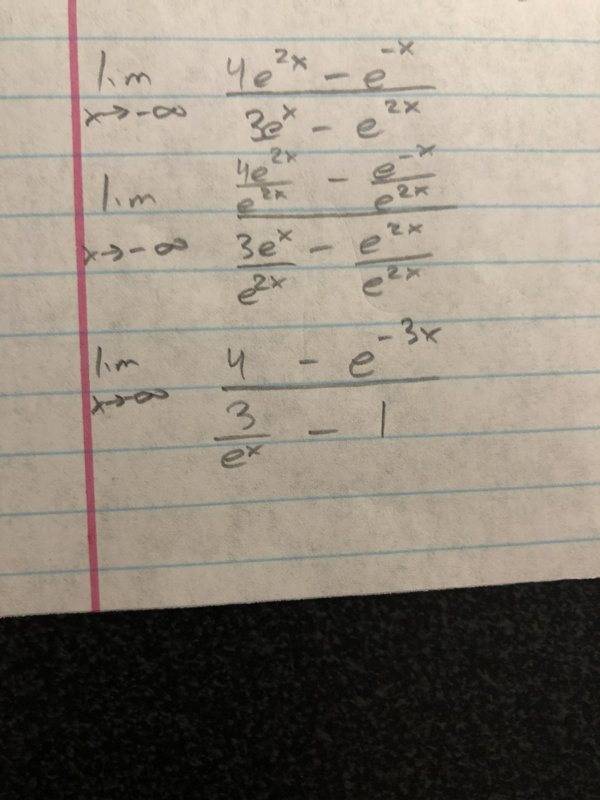SUMMARY
The discussion focuses on solving the limit as x approaches negative infinity for the expression limx→−∞(4e2x - e−x) / (3ex - e2x). Participants clarify that as x tends to negative infinity, the term e−x grows significantly, while e2x approaches zero. The final limit evaluates to -1/3, confirming that the answer is not finite. Proper simplification techniques are emphasized to avoid losing critical information during calculations.
PREREQUISITES
- Understanding of limits in calculus
- Familiarity with exponential functions
- Knowledge of L'Hôpital's Rule for indeterminate forms
- Ability to manipulate algebraic expressions involving exponents
NEXT STEPS
- Study the application of L'Hôpital's Rule for limits involving exponential functions
- Learn how to simplify complex fractions in limit problems
- Explore the behavior of exponential functions as x approaches positive and negative infinity
- Practice solving various limit problems to reinforce understanding of limit concepts
USEFUL FOR
Students studying calculus, particularly those tackling limits and exponential functions, as well as educators looking for examples to illustrate limit-solving techniques.