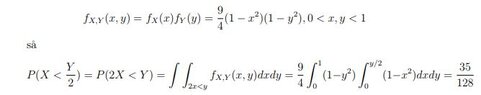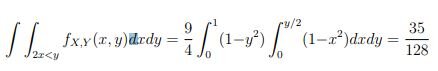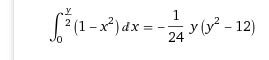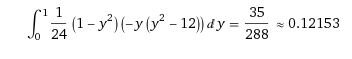Discussion Overview
The discussion revolves around solving a double integral involving two variables, where participants share their approaches, calculations, and results. The focus is on the integration process and the discrepancies observed between hand calculations and results obtained from an online calculator.
Discussion Character
- Mathematical reasoning, Debate/contested
Main Points Raised
- One participant expresses confusion over the integral's format and attempts to integrate in different orders without success.
- Another participant provides a detailed calculation of the integral, arriving at a specific numerical result.
- A third participant confirms the calculations but notes a discrepancy when comparing results with an online calculator, suggesting a potential error in hand calculations.
- Further discussion reveals that the same participant cannot find an error in their calculations, leading to uncertainty about the differences in results.
- Another participant points out a possible sign error in the calculations, indicating that it may affect the final result.
- One participant acknowledges the timing of their response in relation to another's post, indicating a collaborative effort in solving the problem.
Areas of Agreement / Disagreement
There is no consensus on the correct result of the integral, as participants have arrived at different answers and are debating the validity of their calculations.
Contextual Notes
Participants express uncertainty regarding the correctness of their hand calculations compared to results from an online calculator, highlighting potential issues with arithmetic or sign errors.