Did Math DF's integral calculator make a glaring mistake?

[SmartyPants]

TL;DR Summary

Used Math DF's integral calculator to check a solution I got, and I think it might be making a big mistake in its calculations...

In calculating the integral $\int{\ln\left(x\right)\,\sin\left(x\right)\,\cos\left(2\,x\right)}{\;\mathrm{d}x}$, I used a few online integral calculators to check my answer. According to one calculator, I got the correct antiderivative, but according to another (Math DF Integral Calculator), I did not.

As you know, the antiderivative of a function can often take more than one form (and sometimes several forms) depending on how one goes about solving the integral. For instance, we know that $\int tan~x~dx$ = both $ln\left | sec~x \right |+C$ and $-ln\left | cos~x \right |+C$. And while it may be straightforward to show that these two solutions are equivalent, it remains to be seen as to whether the two different solutions these online integral calculators came up with for $\int{\ln\left(x\right)\,\sin\left(x\right)\,\cos\left(2\,x\right)}{\;\mathrm{d}x}$ are in fact equivalent.

But for the moment, I'm more concerned with whether or not Math DF's integral calculator got it wrong than I am concerned with showing that two different solutions to $\int{\ln\left(x\right)\,\sin\left(x\right)\,\cos\left(2\,x\right)}{\;\mathrm{d}x}$ are equivalent. Math DF's solution is as follows (it'll be easier for me to just post screen shots than it will to put it all in LaTex code here, as some of the LateX code at Math DF can be copied, but much of it can't be copied):

The calculator chooses to go with Integration by Parts to start, and right away, in breaking the integrand up into a $u$ and a $dv$, it doesn't account for the entire integrand. Specifically, it chooses $u=sin~x$ and $dv=cos~2x~dx$, and leaves the $ln~x$ out completely. These IBP calculations would make sense for $\int sin~x~cos~2x~dx$, but not for $\int{\ln\left(x\right)\,\sin\left(x\right)\,\cos\left(2\,x\right)}{\;\mathrm{d}x}$...unless am I overlooking something.

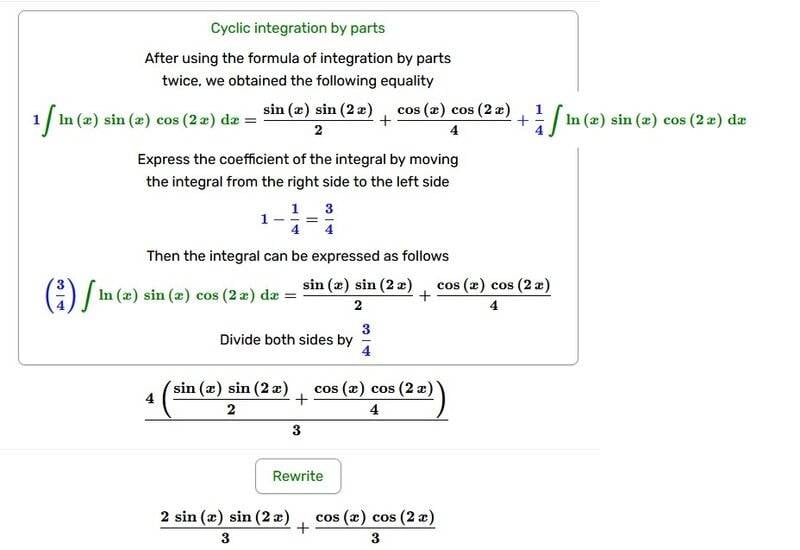
As for this second part of their solution, the calculations I see here seem to make good sense so long as the calculations that got them to this point (performing IBP twice) are correct. But again, I can't be sure that this calculation is correct because I don't know that they got their integration by parts correct in the first place...and on the surface, it appears that they got the IBP calculations wrong.

In summary, are their IBP calculations correct and am I just overlooking something simple? Or did Math DF's integral calculator make a blatant error in leaving the $ln~x$ out of their IBP calculations?

Thanks in advance,
Eric

 

[Mark44]

As you know, the antiderivative of a function can often take more than one form (and sometimes several forms) depending on how one goes about solving the integral.

Yes. For a different example, for the indefinite integral $\int \sin(x)dx$, both $\frac 1 2 \sin^2(x) + C$ and $-\frac 1 2 \cos^2(x) + C$ are correct antiderivatives. However, but I wouldn't call the different results "equivalent." For a fixed C, these two results will give different answers. What is true, though, is that the two functions differ by at most a constant; i.e., $\frac 1 2\sin^2(x) = -\frac 1 2\cos^2(x) + \frac 1 2$. What else is true is that both have equal derivatives.

If two integration techniques result in different answers, you can confirm that they are correct by differentiating both. If both are correct, both derivatives will be equal.

 

[SmartyPants]

Yes. For a different example, for the indefinite integral $\int \sin(x)dx$, both $\frac 1 2 \sin^2(x) + C$ and $-\frac 1 2 \cos^2(x) + C$ are correct antiderivatives. However, but I wouldn't call the different results "equivalent." For a fixed C, these two results will give different answers. What is true, though, is that the two functions differ by at most a constant; i.e., $\frac 1 2\sin^2(x) = -\frac 1 2\cos^2(x) + \frac 1 2$. What else is true is that both have equal derivatives.

If two integration techniques result in different answers, you can confirm that they are correct by differentiating both. If both are correct, both derivatives will be equal.

Thanks for clarifying that much Mark. That makes much more sense, as I don't know that $ln\left | sec~x \right |$ (an antiderivative of $tan~x$) can be manipulated into $-ln\left | cos~x \right |$ if the constants of integration are left out.

That said, as I mentioned before, I'm not particularly interested in showing that the two different results are both valid by differentiating them both and seeing if I come up with the same derivative. Rather I just want to know if Math DF's calculation of $\int{\ln\left(x\right)\,\sin\left(x\right)\,\cos\left(2\,x\right)}{\;\mathrm{d}x}$ is correct, particularly their Integration by Parts calculations, because at first glance it appears to be incorrect with the way they leave $ln~x$ out of the calculation entirely.

 

[Mark44]

Thanks for clarifying that much Mark. That makes much more sense, as I don't know that $ln\left | sec~x \right |$ (an antiderivative of $tan~x$) can be manipulated into $-ln\left | cos~x \right |$ if the constants of integration are left out.

$\ln |\sec(x)| = \ln \frac 1{|\cos(x)|} = -\ln|\cos(x)|$
In this case, the different results are exactly equal.

That said, as I mentioned before, I'm not particularly interested in showing that the two different results are both valid by differentiating them both and seeing if I come up with the same derivative. Rather I just want to know if Math DF's calculation of $\int{\ln\left(x\right)\,\sin\left(x\right)\,\cos\left(2\,x\right)}{\;\mathrm{d}x}$ is correct, particularly their Integration by Parts calculations, because at first glance it appears to be incorrect with the way they leave $ln~x$ out of the calculation entirely.

Seems to me that it would be easier to verify that their results are correct by differentiating than to try to ferret out a possible mistake in their work...

 

[SmartyPants]

Seems to me that it would be easier to verify that their results are correct by differentiating than to try to ferret out a possible mistake in their work...

Agreed...but even if I could show that two different antiderivatives have the same derivative, that doesn't help me understand how Math DF performed integration by parts in this particular example.

IBP is simple: $\int u~dv = uv-\int v~du$. When performing it, one must choose a $u$ and a $dv$, and $u~dv$ must represent the entire integrand ($ln~x~sin~x~cos~2x~dx$), not just part of it ($sin~x~cos~2x~dx$). Am I incorrect in this regard? Or is this statement true (and is Math DF screwing up its IBP calculation)? It seems to me that Math DF is only integrating part of the original integrand and just throwing back in the part it left out ($ln~x$) after having arrived at an answer for $\int sin~x~cos~2x~dx$.

 

[Mark44]

Agreed...but even if I could show that two different antiderivatives have the same derivative, that doesn't help me understand how Math DF performed integration by parts in this particular example.

Right, but differentiating the two results and arriving at the same integrand should convince you that the technique chosen by Math DF was a valid one. If the two results didn't result in the same integrand, then you could see where they went wrong in their IBP technique.

IBP is simple: $\int u~dv = uv-\int v~du$. When performing it, one must choose a $u$ and a $dv$, and $u~dv$ must represent the entire integrand ($ln~x~sin~x~cos~2x~dx$), not just part of it ($sin~x~cos~2x~dx$). Am I incorrect in this regard?

No, that is correct.

Or is this statement true (and is Math DF screwing up its IBP calculation)? It seems to me that Math DF is only integrating part of the original integrand and just throwing back in the part it left out ($ln~x$) after having arrived at an answer for $\int sin~x~cos~2x~dx$.

It's hard to say whether Math DF is screwing up, as the image you attached in post 1 doesn't show the complete equation in the first equation they show. This is the one in which the left side is $1\int \ln(x)\sin(x)\cos(2x)dx = \dots$ and the right side looks like $\dots + \frac 1 4 \int 1$. That final character looks like the digit '1' but probably is 'l' (lower case L). I have not written the two fractional quantities that precede this integral. The complete final integral has to be $\frac 1 4 \int \ln(x)\sin(x)\cos(2x)dx$.

As it says in the image, they have performed IBP twice, but it's difficult to determine exactly which substitutions they have used in each one.

Here's a link to a web page on integration by parts that includes a couple of examples where repeated IBP is appropriate - https://math.berkeley.edu/~ehallman/math1B/IntByParts.pdf.

 

[pasmith]

Yes, it's a bug. It only calculates $\int \sin x \cos 2x\,dx$ by integrating by parts twice; the $\ln (x)$ is completely ignored. It's not an issue with having three factors in the integrand, since it seems to do $\int x \sin x \cos 2x\,dx$ correctly.

You can simplify the integrand by using $$\sin x \cos 2x = \frac12 (\sin 3x - \sin x).$$ The calculator does produce the correct answer for $\int \ln x \sin ax\,dx$.

 

[SmartyPants]

It's hard to say whether Math DF is screwing up, as the image you attached in post 1 doesn't show the complete equation in the first equation they show. This is the one in which the left side is $1\int \ln(x)\sin(x)\cos(2x)dx = \dots$ and the right side looks like $\dots + \frac 1 4 \int 1$. That final character looks like the digit '1' but probably is 'l' (lower case L). I have not written the two fractional quantities that precede this integral. The complete final integral has to be $\frac 1 4 \int \ln(x)\sin(x)\cos(2x)dx$.

As it says in the image, they have performed IBP twice, but it's difficult to determine exactly which substitutions they have used in each one.

Here's a link to a web page on integration by parts that includes a couple of examples where repeated IBP is appropriate - https://math.berkeley.edu/~ehallman/math1B/IntByParts.pdf.

Hmm...I doctored that image to show the entire equation before posting it...weird that it's not showing you the entire equation. At any rate, you are correct - the part that got cut off is $\frac 1 4 \int \ln(x)\sin(x)\cos(2x)dx$. Also, the picture does show what substitutions were made for $u$ and $dv$ in each IBP it performed, right in each "integration by parts" box...unless that part of the first picture got cut off as well.

 

[SmartyPants]

Yes, it's a bug. It only calculates $\int \sin x \cos 2x\,dx$ by integrating by parts twice; the $\ln (x)$ is completely ignored. It's not an issue with having three factors in the integrand, since it seems to do $\int x \sin x \cos 2x\,dx$ correctly.

You can simplify the integrand by using $$\sin x \cos 2x = \frac12 (\sin 3x - \sin x).$$ The calculator does produce the correct answer for $\int \ln x \sin ax\,dx$.

$\sin x \cos 2x = \frac12 (\sin 3x - \sin x)$ - this is the trig manipulation I used to get to the final solution. And thank you for confirming for me that Math DF appears to be leaving something out of the IBP calculations, or at the very least skipping a number of steps that I wasn't able to visualize in my head. Math DF tends to sometimes skip steps that might be obvious to Albert Einstein, Terrence Tao, and Richard Feynman, while not realizing that they aren't always obvious to us mere mortals LOL. I just wanted to make sure that I wasn't going crazy haha.

*EDIT* - Also, I did exactly what you did and replaced $ln~x$ with $x$, calculated $\int x \sin x \cos 2x\,dx$, and it did that one correctly...who knows why it's leaving the $ln~x$ out of the other integral.