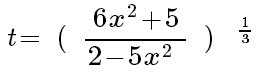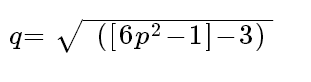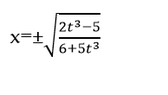- #1
How Do You Transpose the Data Shown in These Pictures?
- Context: MHB
- Thread starter vb14
- Start date
-
- Tags
- Transpose
Click For Summary
Discussion Overview
The discussion revolves around the process of transposing equations presented in attached pictures. Participants seek assistance with mathematical manipulations, specifically focusing on algebraic transformations and solving for variables.
Discussion Character
- Homework-related, Mathematical reasoning, Technical explanation
Main Points Raised
- One participant requests help to transpose data from attached pictures.
- Another participant simplifies an equation to express one variable in terms of another, providing step-by-step transformations.
- A participant asks for assistance with a second equation, indicating a need for further clarification.
- Another participant suggests cubing both sides of an equation to eliminate a rational exponent and provides a subsequent manipulation of the equation.
- A participant questions the origin of a variable in a previous post and offers a method to rearrange the equation for solving.
- One participant confirms the correctness of a solution provided by another and inquires about the understanding of the process.
Areas of Agreement / Disagreement
Participants generally engage collaboratively, with some confirming the correctness of steps taken, but there is no explicit consensus on all aspects of the transposition process.
Contextual Notes
Some steps in the mathematical manipulations remain unresolved, and there are dependencies on the definitions of variables and the context of the equations presented in the pictures.
Who May Find This Useful
Readers interested in algebraic manipulation, equation transposition, and collaborative problem-solving in mathematics may find this discussion beneficial.
- #2
Sudharaka
Gold Member
MHB
- 1,558
- 1
vb14 said:
Hi vb14, :)
Welcome to MHB! The first equation can be simplified to,
$$q=\sqrt{6p^2-4}$$
Now square both sides to get,
$$q^2=6p^2-4$$
Add $4$ to both sides,
$$q^2+4=6p^2$$
Divide both sides by $6$,
$$\frac{q^2+4}{6}=p^2$$
Take the square root of both sides,
$$p=\pm\sqrt{\frac{q^2+4}{6}}$$
Can you give it a try for the second one?
- #3
vb14
- 8
- 0
can you give a hand with second one as well?
please:)
please:)
- #4
MarkFL
Gold Member
MHB
- 13,284
- 12
Start by cubing both sides to get rid of the rational exponent on the right side...what do you have now?
- #5
vb14
- 8
- 0
2x-5x2=(6x2+5)/t3
- #6
MarkFL
Gold Member
MHB
- 13,284
- 12
Where did the $x$ on the left side come from?
I would first just write:
$$t^3=\frac{6x^2+5}{2-5x^2}$$
Next, multiply through by $2-5x^2$ to get:
$$2t^3-5t^3x^2=6x^2+5$$
Now, what you want to do is arrange the equation with all the terms involving $x$ on one side and everything else on the other, the factor out $x^2$ and divide through by the other factor to solve for $x^2$ and then take the square root of both sides.
edit: I see you have also posted this at MMF and have been given the solution.
I would first just write:
$$t^3=\frac{6x^2+5}{2-5x^2}$$
Next, multiply through by $2-5x^2$ to get:
$$2t^3-5t^3x^2=6x^2+5$$
Now, what you want to do is arrange the equation with all the terms involving $x$ on one side and everything else on the other, the factor out $x^2$ and divide through by the other factor to solve for $x^2$ and then take the square root of both sides.
edit: I see you have also posted this at MMF and have been given the solution.
- #7
- #8
MarkFL
Gold Member
MHB
- 13,284
- 12
Yes, that is correct. Do you understand how that was obtained?
Similar threads
- · Replies 3 ·
- · Replies 1 ·
- · Replies 2 ·
High School
What would you call this sample?
- · Replies 9 ·
- · Replies 14 ·
- · Replies 2 ·
- · Replies 6 ·
High School
Transposing Formula: How to Make "l" the Subject
- · Replies 3 ·
- · Replies 7 ·
- · Replies 3 ·