How Does a Vibrating Sample Magnetometer Calculate Magnetic Moment?

In summary, the conversation discusses a VSM (Vibrating Sample Magnetometer) and the equation for induced voltage in a coil, where the induced voltage is shown to be equal to the negative derivative of magnetic flux with respect to time. The conversation then moves on to discussing a solution for this equation, which involves defining z as the position of the coil and using trigonometric functions to find the derivative of z with respect to time. It is mentioned that the magnetic moment is equal to or proportional to m, and that this may be an approximation based on small amplitude oscillations and linear dependence. The conversation concludes with a question about the concept of a VSM and its potential use as a rotating coil in a magnetic field.
  • #1
no_einstein
2
0
TL;DR Summary
How do you find the change in flux with respect to position
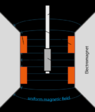
In descriptions of a VSM, the induced voltage in a coil is shown to be emf = -dPhi/dt = - (dPhi/dz)(dz/dt). From here, everyone seem to jump to a solution of emf = 2*Pi*A*f*m*sin(2*Pi*f*t).
That makes some sense: in this case, you can define z = A*cos(2*Pi*f*t) so (dz/dt) = 2*Pi*A*f*sin(2*Pi*f*t). I'm confused why (dPhi/dz) turns out to be equal to or proportional to m (the magnetic moment). Is it an approximation that assumes a small amplitude of oscillation and so a linear dependence of the magnetic flux on z? I am having trouble picturing this. Can someone help?
 
Physics news on Phys.org
  • #2
What is a "VSM"? Is it a rotating coil in a magnetic field?
 
  • #3
vanhees71 said:
What is a "VSM"? Is it a rotating coil in a magnetic field?
I guess it's his Vibrating Sample Magnetometer -- a quick search of Google Images turns up this:

1666717336498.png


https://en.wikipedia.org/wiki/Vibrating-sample_magnetometer
 

Attachments

  • 1666717315037.png
    1666717315037.png
    4 KB · Views: 107
  • Informative
Likes vanhees71

FAQ: How Does a Vibrating Sample Magnetometer Calculate Magnetic Moment?

What is a Vibrating Sample Magnetometer (VSM)?

A Vibrating Sample Magnetometer (VSM) is a scientific instrument used to measure the magnetic properties of materials. It consists of a sample holder, an electromagnet, and a sensing coil. The sample holder is attached to a vibrating platform, which allows for precise measurement of the magnetic properties of the sample.

How does a VSM work?

A VSM works by applying a magnetic field to a sample and measuring the magnetic response of the sample. The sample is attached to the vibrating platform and placed inside the electromagnet. As the magnetic field is changed, the sample will vibrate at a different frequency, which is detected by the sensing coil. This frequency is then used to calculate the magnetic properties of the sample.

What are the advantages of using a VSM?

One of the main advantages of using a VSM is its high sensitivity. It can detect very small changes in the magnetic properties of a sample, making it useful for studying materials with weak magnetic properties. It also allows for precise measurement of the magnetic properties, making it a valuable tool for researchers in various fields such as materials science, physics, and geology.

What types of materials can be studied with a VSM?

A VSM can be used to study a wide range of materials, including metals, alloys, ceramics, and minerals. It can also be used to study thin films and nanoparticles. The magnetic properties that can be measured include magnetization, magnetic susceptibility, and coercivity.

Are there any limitations to using a VSM?

One limitation of using a VSM is that it requires the sample to be in a solid state. It cannot be used to study liquids or gases. Additionally, the sample size must be small enough to fit inside the sample holder, which may limit the types of samples that can be studied. Finally, the VSM is sensitive to external vibrations and magnetic fields, so it must be operated in a controlled environment to obtain accurate results.

Similar threads

I How induction works within a coil (nuances of it)
Replies
6
Views
451
Loop falling in a magnetic field
Replies
4
Views
2K
Lorentz force and induced electric field
Replies
6
Views
673
I Derivative of the retarded vector potential
Replies
1
Views
1K
Current induced on a coil by a changing magnetic flux in another coil
Replies
5
Views
2K
Interaction between a neutral atom and an external magnetic field
Replies
2
Views
2K
Maximum Angular Velocity of an Electric Motor
Replies
2
Views
4K
Calculating multiple magnitudes for induced electric field
Replies
1
Views
2K
Where Can I Find an Affordable Vibrating Sample Magnetometer Head?
Replies
2
Views
3K
Engineering How can I find this formula for the magnetic flux density? (EMagn)
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top