Emspak
- 240
- 1
A U-shaped Tube problem...
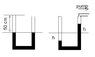
A u-shaped tube with a 1 square centimeter cross-section is filled with mercury to a depth of 50 centimeters on each side.
One side is capped and the air pressure is 750 Torr. The other side is connected to a vacuum pump.
a) how far does the mercury in the dupe drop on the left side? b) what is the final pressure of the air there?
(We are assuming a constant temperature)
I'm using the old perfect gas law, PV = constant.
OK, so I know that the mercury will move h centimeters on one side (down) and h on the other (up). So the total distance the mercury moves is 2h.
If I assume that the pressure in the part of the tube where the air is starts at P0V0and goes to P<sub>final</sub>V<sub>final</sub> I can do this: <br /> <br /> P_0V_0 = P_{final}V_{final} because both PVs = nRT. <br /> <br /> I also know that the pressure exerted by the mercury is 50{\rho}_{Hg} because there are 50 centimeters worth of it at the start. <br /> <br /> Since the pressure of the air increases the volume on the left side I know that <br /> <br /> P_{final}V_{final} = P_{final}(V_0+h) and since the cross section is 1 cm<sup>2</sup> we don't have to worry about area here, it's just 1. <br /> <br /> Meanwhile, the mercury will (once everything settles to equilibrium) exerts the same pressure, but it will be {\rho}_{Hg}(50+2h).<br /> <br /> That should give me P_{final}V_{final} = P_{final}(V_0+h) = {\rho}_{Hg}(50+2h)(50+2h) and since we know V<sub>0</sub> (It's 50) then: <br /> <br /> P_{final}V_{final} = P_{final}(50+h) = (50{\rho}_{Hg}+2h{\rho}_{Hg})(50+2h) <br /> <br /> And this is where I suspect I am going wrong. Or maybe I just did something algebraically that messed it up. I don't thnik I should be getting h<sup>2</sup> factors. <br /> <br /> I know the answer it supposed to be 25 centimeters and 500 Torr for the pressure of the air. And sort of intuitively I know it. But I am trying to work this out correctly. I've seen similar problems on the forum here but none quite like this.<br /> <br /> EDIT: thanks in advance.
Homework Statement
A u-shaped tube with a 1 square centimeter cross-section is filled with mercury to a depth of 50 centimeters on each side.
One side is capped and the air pressure is 750 Torr. The other side is connected to a vacuum pump.
a) how far does the mercury in the dupe drop on the left side? b) what is the final pressure of the air there?
(We are assuming a constant temperature)
Homework Equations
I'm using the old perfect gas law, PV = constant.
The Attempt at a Solution
OK, so I know that the mercury will move h centimeters on one side (down) and h on the other (up). So the total distance the mercury moves is 2h.
If I assume that the pressure in the part of the tube where the air is starts at P0V0and goes to P<sub>final</sub>V<sub>final</sub> I can do this: <br /> <br /> P_0V_0 = P_{final}V_{final} because both PVs = nRT. <br /> <br /> I also know that the pressure exerted by the mercury is 50{\rho}_{Hg} because there are 50 centimeters worth of it at the start. <br /> <br /> Since the pressure of the air increases the volume on the left side I know that <br /> <br /> P_{final}V_{final} = P_{final}(V_0+h) and since the cross section is 1 cm<sup>2</sup> we don't have to worry about area here, it's just 1. <br /> <br /> Meanwhile, the mercury will (once everything settles to equilibrium) exerts the same pressure, but it will be {\rho}_{Hg}(50+2h).<br /> <br /> That should give me P_{final}V_{final} = P_{final}(V_0+h) = {\rho}_{Hg}(50+2h)(50+2h) and since we know V<sub>0</sub> (It's 50) then: <br /> <br /> P_{final}V_{final} = P_{final}(50+h) = (50{\rho}_{Hg}+2h{\rho}_{Hg})(50+2h) <br /> <br /> And this is where I suspect I am going wrong. Or maybe I just did something algebraically that messed it up. I don't thnik I should be getting h<sup>2</sup> factors. <br /> <br /> I know the answer it supposed to be 25 centimeters and 500 Torr for the pressure of the air. And sort of intuitively I know it. But I am trying to work this out correctly. I've seen similar problems on the forum here but none quite like this.<br /> <br /> EDIT: thanks in advance.