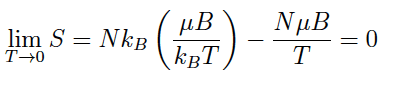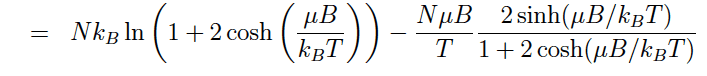SUMMARY
The discussion centers on the limits of the hyperbolic functions sinh and cosh as x approaches infinity. It is established that both sinh(x) and cosh(x) approach e^x, leading to the conclusion that the term 1 becomes negligible compared to the cosh term. Additionally, as T approaches 0, the expression ln(1 + 2cosh(μB/kBT)) simplifies to μB/kBT, confirming the behavior of these functions in the limit. The mathematical representation of cosh(x) as (e^x + e^(-x))/2 is also highlighted, emphasizing the dominance of the e^x term.
PREREQUISITES
- Understanding of hyperbolic functions, specifically sinh and cosh.
- Familiarity with limits in calculus, particularly limits approaching infinity.
- Knowledge of logarithmic functions and their properties.
- Basic concepts of statistical mechanics, including the Boltzmann constant (kB) and magnetic moment (μ).
NEXT STEPS
- Study the behavior of exponential functions as x approaches infinity.
- Learn about the applications of hyperbolic functions in physics and engineering.
- Explore the derivation and implications of the limit properties of logarithmic functions.
- Investigate the role of the Boltzmann constant in statistical mechanics and thermodynamics.
USEFUL FOR
Students and professionals in mathematics, physics, and engineering who are interested in understanding the limits of hyperbolic functions and their applications in statistical mechanics.