Discussion Overview
The discussion revolves around the behavior of the sum of random signals as the number of signals increases, particularly focusing on how the sum appears to flatten out. Participants explore the implications of the Law of Large Numbers and the characteristics of the signals involved, including their phases and amplitudes.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
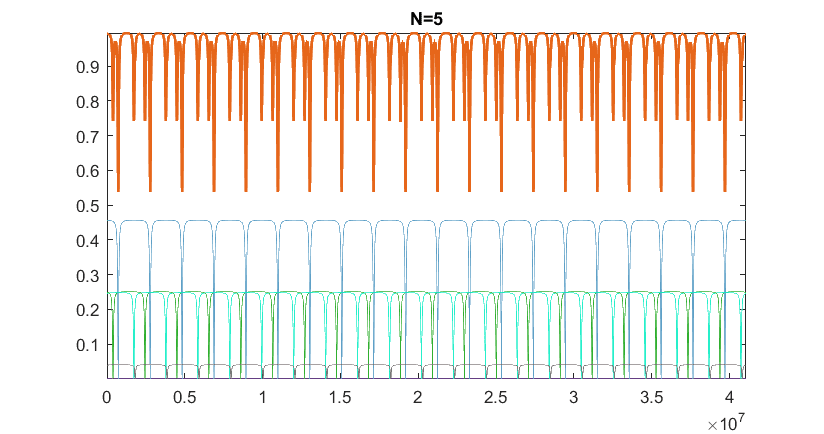
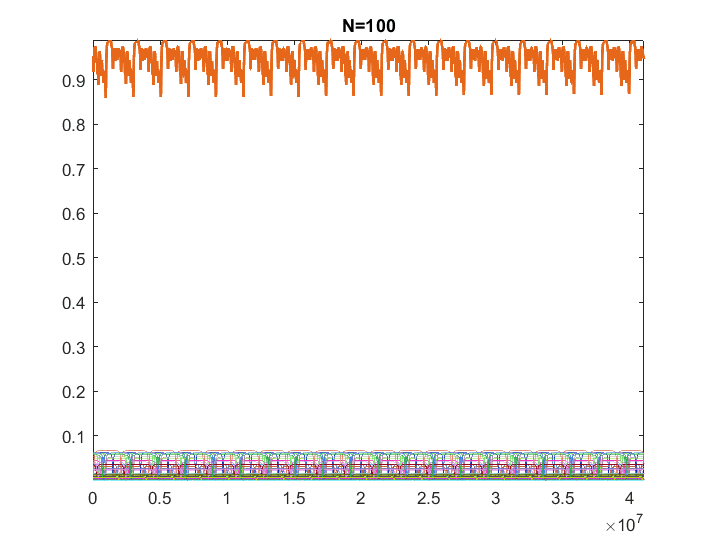
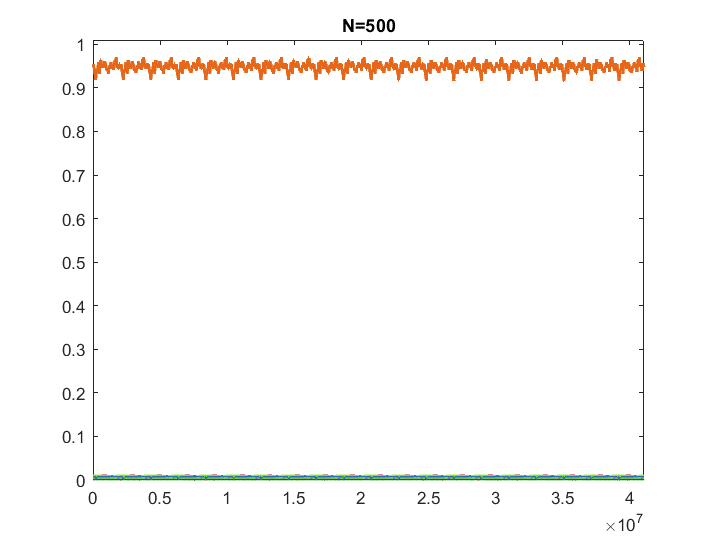
- Some participants present simulations showing that the sum of signals with random phases and amplitudes tends to flatten as the number of signals increases.
- One participant notes that the sum of the amplitudes must be finite, while another confirms that their simulations maintain a maximum amplitude of 1.
- Several participants suggest that the Law of Large Numbers may explain why the average of independent random variables approaches a specific value as the number of samples increases.
- There is a discussion about the distribution of phases and amplitudes, with one participant describing the phases as uniformly distributed and the amplitudes as sampled from an exponential distribution.
- One participant questions how to ensure the sum of the amplitudes equals 1 while drawing independently from an exponential distribution.
- Another participant introduces the concept of periodicity and the relationship between the phase and frequency of the signals, referencing the Airy function and its application in a Fabry-Perot etalon.
- One participant expresses uncertainty about whether the sum will truly flatten or if it may appear smaller due to time limitations.
Areas of Agreement / Disagreement
Participants express a range of views on the behavior of the sum of signals, with some supporting the idea that it flattens out while others raise questions about the underlying assumptions and definitions. The discussion remains unresolved regarding the formal mathematical justification for the observed flattening effect.
Contextual Notes
Participants note the need for clarity on the definitions of the signals and the procedures used to generate them, as well as the implications of finite sums and the distribution of amplitudes and phases.