How Does Torque Affect Angular Acceleration in a Circular Disk?

[ac7597]

Homework Statement

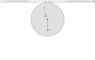
Fred makes a circular disk of copper, with mass m=1.1 kg and radius R=0.96 meters. He drills a hole at the spot marked "X", which is 0.75 of the way from the center to the edge of the disk. He then suspends the disk from a nail, so that the disk is free to rotate around the nail.

What is the moment of inertia of the disk around the nail?

Fred now swings the disk by a small angle of θ=9.8 degrees, as shown in the diagram below. He holds the disk in this position.

What is the angular displacement from its original position? Provide the answer in radians, and use a positive value to mean "into the page" and a negative value to mean "out of the page."

In this position, what is the torque around the nail due to gravity? Use a positive value to mean "into the page" and a negative value to mean "out of the page."

Fred now releases the disk. It starts to swing back to its original orientation.
What is the initial angular acceleration of the disk?

Relevant Equations

torque= Force * radius * sin(theta)

moment of inertia= [(1/2)(1.1kg)(0.96)^2+ (1.1kg) (0.75*0.96)^2]= 1.08 kg*m^2
θ=9.8 degrees= 0.17 rad

torque= (mass*gravity) * radius * sin(theta)
radius= 0.17rad * 0.96m = 0.16m
torque= (1.1kg*9.8m/s^2) * 0.16m * sin(0.17rad) = 0.29 N*m

torque = inertia * angular acceleration
0.29N*m= 1.08 kg*m^2 * angular acceleration
angular acceleration = 0.27 rad/s^2

 

[kuruman]

Are you posting a solution to a problem that interests you or do you have a question to ask?

 

[ac7597]

Hello,
the torque is incorrect for some reason.

 

[kuruman]

Hello,
the torque is incorrect for some reason.

Check your premises. The reason is that one of the items that goes in the torque calculation is incorrect.

 

[ac7597]

the radius?
Should radius= 0.96m ?

 

[haruspex]

θ=9.8 degrees= 0.17 rad

Did you take this instruction into account?
... use a positive value to mean "into the page"
If so, what rule did you use to determine whether it was into the page?

torque= (mass*gravity) * radius * sin(theta)

In the context of that as a general equation, what does "radius" refer to?

 

[ac7597]

radius is the distance from x to the origin so (3/4)*0.96m
by the the right hand rule the torque points into the page thus it is positive:
torque= (1.1*9.8) * (3/4)*0.96 * sin(0.17rad)= 1.32 N*m ?

 

[ac7597]

Is it -1.32N*m?

 

[haruspex]

radius is the distance from x to the origin so (3/4)*0.96m
by the the right hand rule the torque points into the page thus it is positive:
torque= (1.1*9.8) * (3/4)*0.96 * sin(0.17rad)= 1.32 N*m ?

Looks right.

Is it -1.32N*m?

No, I was just checking you had thought it through.