ognik
- 626
- 2
A method for finding the shortest distance between 2 skew, non intersecting lines is to 1st find the common normal, using $ \vec{n} = \frac{\vec{v_1} \times \vec{v_2}}{|\vec{v_1} \times \vec{v_2}|} $ I'm looking for a proof or intuition as to why this is true please?
Then apparently we get the shortest distance (d) by projecting any distance vector onto this normal? A distance vector here is any point on one vector minus any point on the other vector. I can obviously choose points to get distance vectors of any magnitude. So my 2nd question is, I assume the angles between any position vector and the skew lines effectively minimise the projection?
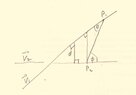
But I did a sketch - View attachment 4918 - which doesn't convince me at all about the above ..., here $|\vec{P_2P_1}| \gt |d|$, multiplying that by $Cos \theta $ produces the line from $P_2 \perp \vec{v_1}$ - still > d?
Then apparently we get the shortest distance (d) by projecting any distance vector onto this normal? A distance vector here is any point on one vector minus any point on the other vector. I can obviously choose points to get distance vectors of any magnitude. So my 2nd question is, I assume the angles between any position vector and the skew lines effectively minimise the projection?
But I did a sketch - View attachment 4918 - which doesn't convince me at all about the above ..., here $|\vec{P_2P_1}| \gt |d|$, multiplying that by $Cos \theta $ produces the line from $P_2 \perp \vec{v_1}$ - still > d?