Arman777 said:
when the ##\Lambda## becomes dominant the universe goes into the inflationary period
No. The inflaton field--the thing that drove the expansion of the universe during inflation--is not the same as ##\Lambda##, the dark energy that is currently driving the universe's accelerated expansion. The dynamics happen to be similar, but that doesn't mean they're the same thing.
Arman777 said:
how can show that increasing the scale factor increases the conformal time
That's not what I said.
You actually wrote down an equation that helps: ##d\eta = dt / a(t)##. Write this as:
$$
\frac{d\eta}{dt} = \frac{1}{a(t)}
$$
In other words, the smaller ##a(t)## is, the more conformal time elapses for a given increment of proper time.
Now consider the interval of proper time from, say, ##10^{-35}## seconds to the proper time of last scattering. This is a fixed interval of proper time. Without inflation, the scale factor would change by some ratio during this interval of proper time; so at the starting proper time, ##10^{-35}## seconds, the scale factor would be smaller than the scale factor at the ending proper time by that ratio--and we know that ending scale factor compared to the scale factor now, that's fixed by observations. Integrating that gives some interval of conformal time.
But
with inflation, the scale factor changes by a much larger ratio from ##10^{-35}## seconds proper time to the proper time of last scattering. So integrating that gives a much larger interval of conformal time, because the scale factor at the start is much smaller (by at least 26 orders of magnitude, or 60 e-foldings).
One thing to bear in mind: the scale factors in the diagram are normalized so the scale factor now is 1. But that means that the actual proper distance now is model-dependent: or, to put it another way, how much proper distance a unit of scale factor corresponds to is model-dependent. It's much, much larger with inflation than without inflation. So a better way to describe the effect of inflation might be to say that it hugely increases the "proper scale factor" (the scale factor in actual proper distance units instead of normalized so the scale factor now = 1) for all times after the end of inflation. And that hugely increases the amount of conformal time that is in the past of all times after the end of inflation. But it doesn't change any conformal times after the end of inflation; so it doesn't move the surface of last scattering relative to now (which is what the diagram in the paper is showing, and why that diagram is wrong); instead, it moves the bottom of the diagram way, way down relative to the surface of last scattering.
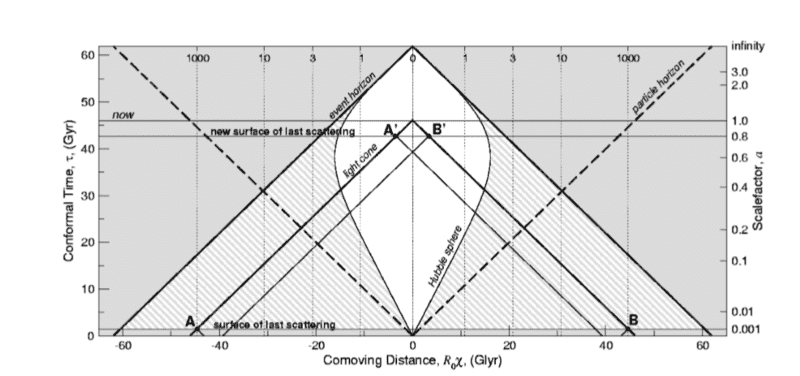 I am having trouble to understand how can shrinking event horizon can lead to a new surface of the last scattering and solve the horizon problem.
I am having trouble to understand how can shrinking event horizon can lead to a new surface of the last scattering and solve the horizon problem.