How high does the ball rise on the non-slip surface?

[annao]

Homework Statement

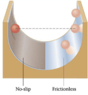
A solid ball with radius of 9.7 cm is released from the height of hs=88.1 cm on a non-slip surface. After reaching its lowest point the ball begins to rise again, on a frictionless surface. How high does the ball rise on that side? Express your answer in cm.

Homework Equations

I=2/5mr^2
Law of conservation of energy: 1/2mv^2 +1/2Iω^2 +mgh=1/2mv^2 +1/2Iω^2 +mgh
ω=sqrt(2mgh/(mr^2+I))
h'=v^2/2g=(rω)^2/2g

The Attempt at a Solution

r=9.7cm =9.7*10^-2m
hs=88.1 cm =0.881m

moment of inertia of ball: I=2/5 mr^2

Law of conservation of energy: 1/2mv^2 +1/2Iω^2 +mgh=1/2mv^2 +1/2Iω^2 +mgh
...
1/2mr^2ω^2 +1/2Iω^2 =mgh

ω=sqrt(2mgh/(mr^2+I))
= sqrt (2mgh/ (mr^2 +2/5mr^2))
= sqrt (2mgh/ mr^2(1+2/5))
= sqrt (2gh/ r^2(1+2/5)

= sqrt(2*9.81m/s^2*0.881m) / (9.7*10^-2m)^2* (1+2/5))
=36.22444194rad/s

h' =v^2/2g
=(rω)^2/2g
=( 9.7*10^-2m*36.22444194rad/s)^2/(2*9.81m/s^2)
=0.6292857143m

Am I doing this problem correctly?

 

[gneill]

Looks okay.

I would probably have let $\omega = \frac{v}{r}$ and solved for $v^2$ at the bottom. Then the conservation of energy for the upslope journey would be pretty trivial.

 

[haruspex]

0.6292857143m

Too many digits, given the initial height is only specified to three digits.
Quickest way is probably to show (or remember) that for a rolling solid ball 5/7 of the KE is linear. So the new height must be 5/7 of the original height.