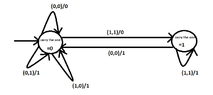
I have thought that we could prove that the dfa is the right one using induction on the length of the given binary numbers.
Suppose that we symbolize with $n$ the length of the given binary numbers.Base case: Let $n=1$. Then we could have the input $(0,0), (0,1), (1,0), (1,1) $.
If the input is $(0,0)$ then the machine prints $0$ which is right, since $0+0=0$.
If the input is $(0,1)$ or $(1,0)$ then the machine prints $1$ which is right since $0+1=1+0=1$.
If the input is $(1,1)$ then the machine prints $0$, which is again right since $1+1=0$ with $1$ to carry over.Induction hypothesis: We suppose that the automaton makes correctly the addition of two binary numbers of length $n$.Induction step: We want to show that the automaton makes correctly the addition of two binary numbers of length $n+1$.
If we have two numbers of length $n+1$, we first add the last $n$ digits.
So we have from the induction hypothesis that the the result of the addition of the last $n$ digits will be right. So from each number, will one digit remain.
If after the addition of the last $n$ digits we are at the first state, it follows from the base case that the result of the addition of the remaining digits will be right.
If after the addition of the last $n$ digits we are at the second state, then we have to remember that we have carried over a 1.
The possible pairs of the remaining digits are these: $(0,0), (1,0), (0,1), (1,1)$.
Suppose that we have $(0,0)$. The machine will print $1$. This is right, since 0+0+carry over =1.
If we have (1,0) or (0,1), then the machine prints $0$, which is again right since 1+0+carry over =0+1+carry over=0+carry over.
If we have (1,1) then the machine prints 1, which is right since 1+1+carry over=1+carry over.
Is it right? Could I improve something?