How Large Must n Be to Guarantee Error Bounds in Approximation Methods?

[MarkFL]

Here is the question:

Consider the definite integral ∫_0^1〖sin⁡(x^2 )dx〗. How large must n be to guarantee that:?

1. |∫_0^1〖sin⁡(x^2 )dx〗- M_n |< .00001
2. |∫_0^1〖sin⁡(x^2 )dx〗- T_n |< .00001
3. |∫_0^1〖sin⁡(x^2 )dx〗- S_n |< .00001
I guess I'm mostly confused on how to find n. Thanks for all your help.

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Courtney,

We are given:

$$I=\int_0^1\sin\left(x^2 \right)\,dx$$

For the definitions of the Error Bound for the 3 methods, we identify:

$$a=0,\,b=1,\,f(x)=\sin\left(x^2 \right)$$

1.) The Error Bound $E_n$ for the Midpoint Rule is:

If there exists a number $M>0$ such that $\left|f''(x) \right|\le M$ for all $x$ in $[a,b]$, then:

$$E_n\le\frac{M(b-a)^3}{24n^2}$$

Using the function given, we find:

$$f''(x)=2\cos\left(x^2 \right)-4x^2\sin\left(x^2 \right)$$

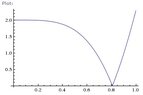
Here is a plot of $y=\left|f''(x) \right|$ on the given interval:

View attachment 1079

We see that:

$$f''(1)=4\sin(1)-2\cos(1)\ge f''(x)$$ for all $x$ in the interval. Thus, we want:

$$\frac{\left(4\sin(1)-2\cos(1) \right)(1-0)^3}{24n^2}<0.00001$$

$$\frac{\left(2\sin(1)-\cos(1) \right)}{12n^2}<\frac{1}{100000}$$

or

$$n^2>\frac{25000}{3}\left(2\sin(1)-\cos(1) \right)\approx9521.99719789711$$

$$97^2<9521.99719789711<98^2$$

Hence, by taking $n\ge98$ we obtain the desired accuracy.

2.) The Error Bound $E_n$ for the Trapezoidal Rule is:

If there exists a number $M>0$ such that $\left|f''(x) \right|\le M$ for all $x$ in $[a,b]$, then:

$$E_n\le\frac{M(b-a)^3}{12n^2}$$

Using the results of 1.) we see that we want:

$$\frac{\left(4\sin(1)-2\cos(1) \right)(1-0)^3}{12n^2}<0.00001$$

$$\frac{\left(2\sin(1)-\cos(1) \right)}{6n^2}<\frac{1}{100000}$$

or

$$n^2>\frac{50000}{3}\left(2\sin(1)-\cos(1) \right)\approx19043.99439579422$$

$$137^2<19043.99439579422<138^2$$

Hence, by taking $n\ge138$ we obtain the desired accuracy.

3.) The Error Bound $E_n$ for Simpson's Rule is:

If there exists a number $M>0$ such that $\left|f^{(4)}(x) \right|\le M$ for all $x$ in $[a,b]$, then:

$$E_n\le\frac{M(b-a)^5}{180n^4}$$

Using the function given, we find:

$$f^{(4)}(x)=4\left(\left(4x^3-3 \right)\sin\left(x^2 \right)-12x^2\cos\left(x^2 \right) \right)$$

Here is a plot of $y=\left|f^{(4)}(x) \right|$ on the given interval along with the absolute maximum:

View attachment 1080

Thus, we want:

$$\frac{28.42851540309637345267676583(1-0)^5}{180n^4}<0.00001$$

$$\frac{28.42851540309637345267676583}{180n^4}<\frac{1}{100000}$$

or

$$n^4>15793.61966838687414037598101\bar{6}$$

$$11^4<15793.61966838687414037598101\bar{6}<12^4$$

Hence, by taking $n\ge12$ we obtain the desired accuracy.