evinda
Gold Member
MHB
- 3,741
- 0
Hello! :)
I am looking at this exercise:
We have these teams : $E_{1},E_{2},...,E_{6}$ . Each team must have a meeting.
How many hours are needed (minimum) so that all the meetings take part, given that:
$$ E_{1}=\{A,B,C\} $$
$$ E_{2}=\{A,D,E\} $$
$$ E_{3}=\{B,C,Z\} $$
$$ E_{4}=\{Z,H,T\} $$
$$ E_{5}=\{E,H\} $$
$$ E_{6}=\{D,E,T\} $$
?
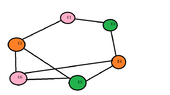
I tried to answer the question with this graph:
View attachment 2545
So, $3$ hours are needed,so that all the meetings take part...
Is it right or have I done something wrong? (Blush)
I am looking at this exercise:
We have these teams : $E_{1},E_{2},...,E_{6}$ . Each team must have a meeting.
How many hours are needed (minimum) so that all the meetings take part, given that:
$$ E_{1}=\{A,B,C\} $$
$$ E_{2}=\{A,D,E\} $$
$$ E_{3}=\{B,C,Z\} $$
$$ E_{4}=\{Z,H,T\} $$
$$ E_{5}=\{E,H\} $$
$$ E_{6}=\{D,E,T\} $$
?
I tried to answer the question with this graph:
View attachment 2545
So, $3$ hours are needed,so that all the meetings take part...
Is it right or have I done something wrong? (Blush)
Attachments
Last edited: