How many kilocalories per gram are there in a 5.00-g peanut?

[member 731016]

Homework Statement

Please see below

Relevant Equations

Conservation of energy

For this,

The solution is,

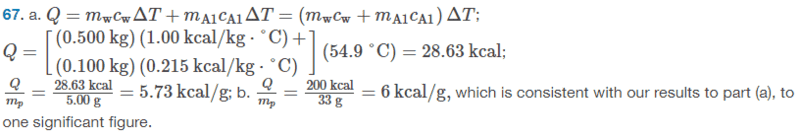
However, I am not sure why they did part(a) like that. I thought we would do it like this:

$Q_{nut} + Q_{w} = 0$ since calorimeter is ideal so energy is conserved in the nut-water system
$Q_{nut} =-Q_{w}$
$Q_{nut} = -(0.500)(4184)(54.9) = -1.15 \times 10^5 J$

Therefore, the heat lost by the nut is $Q_{nut} = 1.15 \times 10^5 J = 27.45 \frac{kcal}{5.00g} = 5.49 \frac{kcal}{g}$

However, I don't understand their method for part(a), is there a mistake in mine?Many thanks!

 

[kuruman]

I think you misunderstood the measurement. For part (a) you generate heat $Q$ by burning 5 g of peanuts. The peanut at this point is gone but the heat is not. The heat is used to raise the temperature of two things, the water and the aluminum container which together form the calorimeter. It is these two that are assumed isolated from the rest of the world so that the heat $Q$ that is pumped into them goes into raising their common temperature by 54.9 °C. You misunderstood in what way the calorimeter is "ideal."

 

[member 731016]

I think you misunderstood the measurement. For part (a) you generate heat $Q$ by burning 5 g of peanuts. The peanut at this point is gone but the heat is not. The heat is used to raise the temperature of two things, the water and the aluminum container which together form the calorimeter. It is these two that are assumed isolated from the rest of the world so that the heat $Q$ that is pumped into them goes into raising their common temperature by 54.9 °C. You misunderstood in what way the calorimeter is "ideal."

Thank you for your reply @kuruman!

That is very helpful. I did not realize that the calorimeter included the aluminum container, so using my method I should have done $Q_{nut} + Q_{w} + Q_{A1} = 0$

 

[kuruman]

Yes.

 

[member 731016]

Yes.

Thank you for your help @kuruman!