How many necklaces can we create?

  • Context: MHB 
  • Thread starter Thread starter mathmari
  • Start date Start date
Click For Summary

Discussion Overview

The discussion revolves around determining the number of distinct necklaces that can be created using $m$ symmetric beads and $k$ colors, utilizing Burnside's Formula. Participants explore the implications of rotations and reflections on the configurations of necklaces, as well as the mathematical underpinnings of the dihedral group associated with these symmetries.

Discussion Character

  • Exploratory
  • Mathematical reasoning
  • Conceptual clarification
  • Debate/contested

Main Points Raised

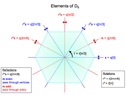
  • Some participants propose that the group $G$ is the dihedral group $D_m$, which accounts for the symmetries of the necklace through rotations and reflections.
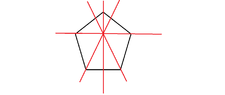
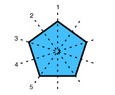
  • There is a discussion about how many configurations remain unchanged under specific rotations, with examples provided using $m=4$ and $m=5$ beads.
  • Participants question how to determine the number of elements that leave a configuration unchanged under various rotations.
  • Some participants suggest that necklaces with all beads of the same color remain unchanged under a rotation by one bead, leading to a count of $k$ such necklaces.
  • Others argue that necklaces with alternating colors can remain unchanged under a rotation by two beads, leading to a count of $k^2$ such necklaces.
  • There is uncertainty about how to generalize these findings for different values of $m$ and the implications for the number of unchanged configurations under various rotations.

Areas of Agreement / Disagreement

Participants express differing views on the implications of rotations and reflections, with no consensus reached on the general method for counting unchanged configurations. The discussion remains unresolved regarding the specific counts for different arrangements and the generalization of these concepts.

Contextual Notes

Limitations include the need for further clarification on the assumptions regarding the arrangements of beads and the definitions of the groups involved. The discussion also highlights unresolved mathematical steps in applying Burnside's Formula to this specific problem.

  • #31
mathmari said:
The second bead and the last but one should also be of the same colour, right?

Right.
So we have AB.BA
 
Physics news on Phys.org
  • #32
I like Serena said:
Right.
So we have AB.BA

So for that reflection there are $k^{\lceil \frac{m}{2}\rceil}$ necklaces that stay unchanged, or not? (Wondering)
 
  • #33
mathmari said:
So for that reflection there are $k^{\lceil \frac{m}{2}\rceil}$ necklaces that stay unchanged, or not? (Wondering)

Yeap.
The axis of symmetry always goes through either 0, 1, or 2 beads.
In all those cases we get $\lceil \frac{m}{2}\rceil$ choices for the color. (Nod)
 
  • #34
I like Serena said:
The axis of symmetry always goes through either 0, 1, or 2 beads.

When the number of beads is odd the axis of symmetry goes through $1$ bead and when the number of beads is even the axis of symmetry goes through $2$ beads, right? (Wondering)

When goes the axis of symmetry through $0$ beads? (Wondering)
 
  • #35
mathmari said:
When the number of beads is odd the axis of symmetry goes through $1$ bead and when the number of beads is even the axis of symmetry goes through $2$ beads, right? (Wondering)

When goes the axis of symmetry through $0$ beads? (Wondering)

Take a look at $D_6$:
View attachment 5402

The axis of symmetry of $s$ in this picture goes through $2$ beads.
The axis of $rs$ goes through $0$ beads. (Thinking)
 

Attachments

  • 4565394280.png
    4565394280.png
    23.2 KB · Views: 114
  • #36
I like Serena said:
Take a look at $D_6$:The axis of symmetry of $s$ in this picture goes through $2$ beads.
The axis of $rs$ goes through $0$ beads. (Thinking)

I got stuck right now... Isn't $m$ constant in this example, $m=6$ ? (Wondering)
How can we take cases if $m$ is odd or even? (Wondering)
 
  • #37
mathmari said:
I got stuck right now... Isn't $m$ constant in this example, $m=6$ ? (Wondering)
How can we take cases if $m$ is odd or even? (Wondering)

I'm afraid $m$ has a different meaning in the picture. (Worried)
In the picture the number of beads is $6$.
And $m$ represents what we called $i$, the number of rotations that we apply.
 
  • #38
I like Serena said:
I'm afraid $m$ has a different meaning in the picture. (Worried)
In the picture the number of beads is $6$.
And $m$ represents what we called $i$, the number of rotations that we apply.

When we have an odd number of beads, would we have again that when the number of reflections is even then the symmetry axis goes through two vertices and when it is odd then the symmetry axis goes through sides? (Wondering)
 
  • #39
mathmari said:
When we have an odd number of beads, would we have again that when the number of reflections is even then the symmetry axis goes through two vertices and when it is odd then the symmetry axis goes through sides? (Wondering)

Suppose we take a look at $D_5$, which is represented by a pentagon.
What would it look like? (Wondering)
 
  • #40
I like Serena said:
Suppose we take a look at $D_5$, which is represented by a pentagon.
What would it look like? (Wondering)

It is of the following form:

View attachment 5403

right? (Wondering)
 

Attachments

  • pent.png
    pent.png
    4.1 KB · Views: 106
  • #41
mathmari said:
It is of the following form:



right? (Wondering)

The vertical line is an axis of symmetry with 2 vertices to the left and 2 to the right.
However, the horizontal line has 1 above and 2 below. (Worried)
 
  • #42
I like Serena said:
The vertical line is an axis of symmetry with 2 vertices to the left and 2 to the right.
However, the horizontal line has 1 above and 2 below. (Worried)

So, when we have an odd number of beads the necklace is unchanged only under the reflection with the vertical line as the axis of symmetry, or not? (Wondering)
Or do we consider also the other two lines as the axis of symmetry of a reflection? (Wondering)
 
  • #43
mathmari said:
So, when we have an odd number of beads the necklace is unchanged only under the reflection with the vertical line as the axis of symmetry, or not? (Wondering)
Or do we consider also the other two lines as the axis of symmetry of a reflection? (Wondering)

The picture should be like:
View attachment 5410

There are 5 axes of symmetry, each intersecting with 1 bead. (Thinking)
 

Attachments

  • 4d9213b908d82fbed032d1ef82b09035.png
    4d9213b908d82fbed032d1ef82b09035.png
    5.5 KB · Views: 113
  • #44
I like Serena said:
The picture should be like:There are 5 axes of symmetry, each intersecting with 1 bead. (Thinking)

Ah ok... I see... (Thinking)

So, when we have an odd number of beads, there are $k^{\lfloor \frac{m}{2}\rfloor+1}=k^{\lceil \frac{m}{2}\rceil}$ necklaces that stay unchanged under a reflection, or not? (Wondering)

And when we have an even number of beads, there are either $k^{\frac{m}{2}}$ necklaces, when we rotate by an odd $i$, or $k^{\frac{m-2}{2}+2}=k^{\frac{m+2}{2}}=k^{\frac{m}{2}+1}$ necklaces, when we rotate by an even $i$ that stay unchanged under a reflection, right? (Wondering)
 
  • #45
Right. (Nod)
 

Similar threads

Undergrad Dfns group action & group, written in terms of the other
  • · Replies 26 ·
Replies
26
Views
1K
MHB Subsets of permutation group: Properties
  • · Replies 18 ·
Replies
18
Views
2K
MHB Convergence of iteration method - Relation between norm and eigenvalue
  • · Replies 2 ·
Replies
2
Views
2K
MHB Show that G is a subset of the symmetric group
  • · Replies 7 ·
Replies
7
Views
2K
MHB How Does Burnside's Lemma Calculate the Number of Distinct Colored Cubes?
  • · Replies 1 ·
Replies
1
Views
2K
MHB Number of Orbits: Showing Equality of Group G and G_a
  • · Replies 34 ·
2
Replies
34
Views
5K
MHB How can we determine the reflection across a given line in Hesse normal form?
  • · Replies 5 ·
Replies
5
Views
2K
MHB How can we prove the equality of orders for finite subgroups of a group?
  • · Replies 8 ·
Replies
8
Views
3K
MHB Show that the intersection is a pp -Sylow subgroup
  • · Replies 3 ·
Replies
3
Views
2K
MHB How to Calculate the Distance Between Parallel Lines in Hesse Normal Form?
  • · Replies 8 ·
Replies
8
Views
3K