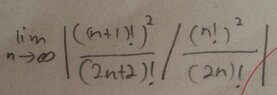How to calculate complicated factorial
- Context: MHB
- Thread starter aruwin
- Start date
-
- Tags
- Factorial
Click For Summary
SUMMARY
This discussion focuses on calculating complicated factorial limits, specifically evaluating the expression involving factorials as n approaches infinity. The key formula discussed is |(n + 1)^2 / ((2n + 2)(2n + 1))|, which simplifies the limit evaluation. Participants emphasize the importance of not substituting infinity directly and recommend expanding brackets and dividing by the highest power of n to identify negligible terms. The correct limit is confirmed to be 1/4.
- Understanding of factorial notation and properties
- Familiarity with limits in calculus
- Ability to manipulate algebraic expressions
- Knowledge of indeterminate forms in calculus
- Learn about evaluating limits involving factorials
- Study the concept of indeterminate forms and L'Hôpital's Rule
- Explore advanced techniques for simplifying complex algebraic expressions
- Investigate the behavior of sequences and series as they approach infinity
Students and professionals in mathematics, particularly those studying calculus and advanced algebra, will benefit from this discussion on factorial limits and evaluation techniques.
Similar threads
- · Replies 4 ·
- · Replies 4 ·
- · Replies 3 ·
- · Replies 7 ·
- · Replies 3 ·
- · Replies 4 ·
- · Replies 9 ·
- · Replies 3 ·