- #1
sams
Gold Member
- 84
- 2
This is not a homework. In Chapter 8: Central-Force Motion, in the Classical Dynamics of Particles and Systems book by Thornton and Marion, Fifth Edition, page 325, Problem 8-19, we are asked to calculate the mass of the planet Saturn. In the instructor's solution manual, the solution for this problem is:
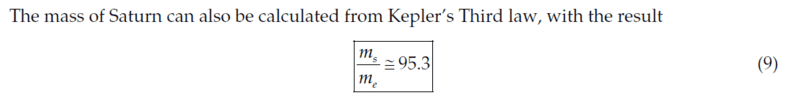
ms is the mass of Saturn.
me is the mass of Earth.
I have tried to write ms and me in terms of the semimajor axis and the period and then dividing ms by me, but I did not obtain the above result!
Could anyone explain how could we obtain this ratio? Any help is much appreciated. Many thanks!
ms is the mass of Saturn.
me is the mass of Earth.
I have tried to write ms and me in terms of the semimajor axis and the period and then dividing ms by me, but I did not obtain the above result!
Could anyone explain how could we obtain this ratio? Any help is much appreciated. Many thanks!