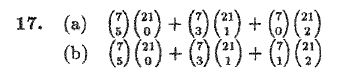jwxie said:
Hi.
Let A = 1,2,3,4,5,6,7
How many symmetric relations on A contain exactly (a) four ordered pairs, (b) 5 , (c) seven and (d) eight
The book has solutions to the first two, which I didn't understand at all.
Please look the pic below
Can someone guide me through how to approach the problem?
Thanks
You can imagine any relation a a table with 7 rows and 7 columns, where you indicate in each position whether the corresponding elements belong to the relation. (This is basically the same as working with the graph of this relation.)
A relation is symmetric if and only if this graph/table is symmetric with respect to the main diagonal. Hence, a symmetric relation is uniquely determined by the pairs on and above the main diagonal.
You have 7 positions on diagonal and 21=6+5+4+3+2+1 positions above the diagonal.
If you put
a elements above the diagonal, then there are also
a elements bellow it, by the symmetry. So, by putting
a elements above the diagonal and
b elements on the diagonal, you obtain a relation consisting of
2a+b pairs.
Now, if you want to have 4 elements you have these possibilities:
all 4 elements are on the diagonal \binom{7}{4};
2 elements on the diagonal and 1 above it \binom72\binom{21}1;
no element on the diagonal and 2 above it \binom{21}2.
For 5 elements you have the following possibilieites:
All 5 elements on the diagonal \binom75;
3 elements on the diagonal and 1 above it \binom73+\binom{21}1;
1 element on the diagonal and 2 above it \binom71+\binom{21}2.