- #1
alik braz
- 4
- 2
hello I am trying to calculate the force applied on the sliders in that sketch
it is a level wind system for winch
I am not an engineer but as much as i understend
the 1000kg load is 10000kn becose it is 1m from the top slider
the sliders at te top are 20 cm apert so the load will be 50000 kn on the slider if it was only slider at the top
but i don't know how the load ditrubot to the bottom sliders and betwen them
ill be very thenkful if somone can explain it to me in simpel way or add link to videos in that sobject
thanks
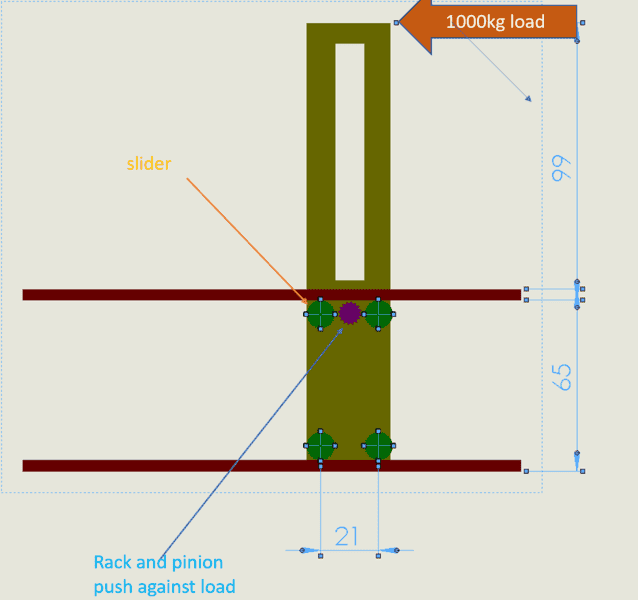
it is a level wind system for winch
I am not an engineer but as much as i understend
the 1000kg load is 10000kn becose it is 1m from the top slider
the sliders at te top are 20 cm apert so the load will be 50000 kn on the slider if it was only slider at the top
but i don't know how the load ditrubot to the bottom sliders and betwen them
ill be very thenkful if somone can explain it to me in simpel way or add link to videos in that sobject
thanks