Discussion Overview
The discussion revolves around the calculation of the pseudoinverse using Singular Value Decomposition (SVD). Participants explore the components of SVD, specifically the matrices U and Vt, and the process of obtaining the pseudoinverse from these matrices. The conversation includes technical clarifications and some confusion regarding the definitions and calculations involved.
Discussion Character
- Technical explanation
- Conceptual clarification
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant expresses uncertainty about the question's requirements, specifically regarding the values of x1, x2, x3, and x4.
- Multiple participants suggest rechecking the determinant related to the expression ##~\mathbf{H^T H - I} \it \lambda ##.
- There is a request for clarification on the meaning of the matrix U and how to derive it along with Vt.
- One participant defines U as a unitary matrix and provides a link for further reading, noting the mathematical property of U being its own inverse when complex.
- Another participant explains that U is part of the SVD representation and discusses the notation differences between Σ and S.
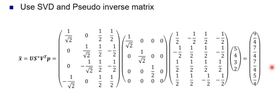
- There is a claim that an image referenced in the discussion incorrectly presents the pseudoinverse calculation, suggesting it should be VS+UT instead of US+VT.
- A question is raised about how to convert the diagonal matrix S to its pseudoinverse S+.
- A response provides a method for obtaining the pseudoinverse of a rectangular diagonal matrix, emphasizing the treatment of small elements in numerical computation.
Areas of Agreement / Disagreement
Participants express varying levels of understanding and agreement on the definitions and calculations related to SVD and the pseudoinverse. There is no clear consensus on the correct representation of the pseudoinverse calculation, indicating ongoing debate.
Contextual Notes
Some participants have corrected their earlier mistakes, but there remain unresolved questions about the definitions and calculations of the matrices involved in SVD and the pseudoinverse. The discussion also highlights potential ambiguities in the mathematical expressions referenced.